С. В. Мельничук
В работе проводится анализ и обсуждается приложение выражения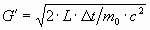 
, где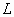 
- светимость и 
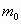- масса, 
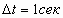. Численное значение 
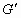для характеристик Солнца, с точностью не хуже двух процентов, совпадает с гравитационной постоянной пониженной размерности, $IMAGE6$. Используя представленное выражение, предлагается техника расчета некоторых основных характеристик звезд, указывающая на взаимосвязь гравитации и электромагнитного излучения. Особенность реализуемого подхода заключается в том, что выражения для численных расчетов масс звезд по их поверхностной температуре получены в аналитическом виде не обращаясь к силам гравитационного взаимодействия. Показано хорошее согласие численных расчетов с экспериментальными данными.
Постановка задачи
Выражение для $IMAGE7$может быть получено исходя из релятивистского соотношения массы
$IMAGE8$(1)
если положить, что в устойчивых термодинамических системах с потерей массы на электромагнитное излучение, таких как звезды, величина $IMAGE9$является мнимой. Данное положение может быть получено строго аналитически, однако рассмотрение этого вопроса является довольно объемным, поэтому выносится за рамки излагаемого материала и используется лишь формальный подход. Тогда:
$IMAGE10$(2)
откуда следует:
$IMAGE11$(3)
при условии, что $IMAGE12$, где $IMAGE13$- масса, теряемая объектом за одну секунду на электромагнитное излучение, 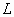- светимость, $IMAGE15$.
Проведем оценку величины (3) для звезд главной последовательности. Для этого воспользуемся известным [1,2] соотношением:
$IMAGE16$(4)
где $IMAGE17$- светимость Солнца, $IMAGE18$- масса Солнца, $IMAGE19$изменяется в пределах $IMAGE20$.
Выполняя несложные преобразования, находим:
$IMAGE21$(5)
Из соотношения (5) следует, что величина 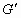не постоянна, а является функцией массы звезд. Данный вывод находится в противоречии с положением о неизменности гравитационной постоянной $IMAGE23$. Следовательно, несмотря на то, что численные значения $IMAGE23$и $IMAGE25$дают хорошее согласие, величину 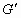нельзя прямо отождествлять с гравитационной постоянной $IMAGE23$. Для того, чтобы установить природу их отличий обратимся к физическому содержанию выражения (3).
Из соотношения (3) следует, что величина 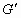непосредственно связана с излучением электромагнитного поля. Это наводит на мысль о возможности построения модели устойчивых термодинамических систем, таких как звезды, не обращаясь к силам гравитационного взаимодействия.
Газокинетическая модель звезд не использующая сил гравитационного взаимодействия
При построении физической модели будем придерживаться положений принятых в литературе [1,2]:
Состояние вещества звезд подчинено законам состояния идеального газа.
Рассматриваемый элементарный объем вещества звезд является абсолютно черным телом.
В соответствии с 1 объемная плотность энергии поступательного движения $IMAGE29$, отвечающая за перенос излучения из центральных областей звезды наружу:
$IMAGE30$(6)
где $IMAGE31$- плотность вещества, $IMAGE32$- средняя молярная масса вещества, $IMAGE33$- газовая постоянная. Объемная плотность энергии электромагнитного излучения переносимого из центральных областей звезды наружу $IMAGE34$:
$IMAGE35$(7)
Рассматривая равенство (6) и (7), как условие стационарности, выразим $IMAGE31$:
$IMAGE37$(8)
Полагая, что источник энергии, переносимой без потерь, является точечным:
$IMAGE38$(9)
приходим к зависимости:
$IMAGE39$(10)
где $IMAGE40$- температура поверхности и радиус звезды. Тогда:
$IMAGE41$(11)
Вычисляя массу вещества, ограниченную объемом радиуса $IMAGE42$находим:
$IMAGE43$(12)
Для Солнца $IMAGE44$. Полагая, что на десять атомов водорода приходится один атом гелия [2], расчет средней молярной массы элементарного объема звездного вещества, в отличие от той же [2], проведем как:
$IMAGE45$
где $IMAGE46$и $IMAGE47$- молярные массы водорода и гелия. Однако, имея в виду [2], применение данного соотношения в совокупности с (6) и (7) нельзя считать однозначным, и требует отдельного, более детального обсуждения.
Выражение (12) для Солнца дает:
$IMAGE48$(13)
Величина с численным значением (13) входит в закон всемирного тяготения, если одной из тяготеющих масс является Солнце, откуда следует:
$IMAGE49$(14)
Полученное значение массы Солнца с хорошей степенью точности совпадает с табличным значением. Данное совпадение дает основание полагать, что используемая физическая модель (6)-(12) с поправкой $IMAGE50$либо $IMAGE51$(пока не определено), верна. Выполняя расчеты масс звезд с помощью установленной процедуры, и сравнивая их с экспериментальными данными, можно выяснить какая из величин $IMAGE23$или 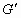определяет истинную поправку. Введем обозначения:
$IMAGE54$(15)
$IMAGE55$(16)
Расчет и сравнение $IMAGE56$и $IMAGE57$проведем на основании экспериментальных данных усредненных характеристик звезд главной последовательности в единицах Солнечных величин. Дальнейшие расчеты будут представлены в этих же единицах.
На рис.1. представлены результаты расчета $IMAGE56$, $IMAGE57$и соответствующие им экспериментальные значения масс в зависимости от светимости на основании данных [3]. Из рис.1. видно, что как выражение (15), так и выражение (16) дают значительное расхождение с экспериментальными данными во всех областях значений, за исключением масс близких к массе Солнца $IMAGE18$. Не сложно заметить, что аналогичная ситуация возникла при численных расчетах величины .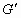
Решая данную проблему, обратим внимание на то, что согласно (1)-(3) звезды с различной массой и светимостью можно рассматривать как инерциальные системы отсчета с отличной от нуля “скоростью относительного движения”. Поэтому, можно ожидать наличия эффектов предсказываемых СТО, а именно: не смотря на то, что с точки зрения наблюдателя Солнечной системы звезды имеют ряд различных параметров, наблюдатели, локализованные возле этих звезд, будут получать значения, некоторых из этих параметров, такие же, как у Солнца.
$IMAGE62$
Если предлагаемая гипотеза верна для гравитационной постоянной, масс и радиусов звезд, а также применим общий принцип относительности к закону всемирного тяготения:
$IMAGE63$(17)
для наблюдателя Солнечной системы массы всех звезд будут одинаковы и равны массе Солнца, только при выполнении условия:
$IMAGE64$(18)
что легко проверить прямой подстановкой экспериментальных данных в полученное соотношение.
На рис.2. круглой меткой представлены экспериментальные данные значений радиусов и квадратной меткой их измененные значения согласно (18) в зависимости от массы звезд главной последовательности. Расчеты и построение проведены на основании экспериментальных данных работы [3]. Из рис.2. видно: соотношение (18) с хорошей точностью выполнимо для значений относительных масс $IMAGE65$, находящихся в интервале $IMAGE66$, что составляет значительную часть звезд главной последовательности. Звезды с характеристиками, не удовлетворяющими соотношению (18), очевидно не соответствуют положениям 1 и 2, сформулированным в начале этого раздела. Тем самым, есть веские основания полагать, что отличие величин $IMAGE23$и 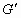имеет релятивистскую природу.
$IMAGE69$
Выполнимость (18) позволяет заключить, что при расчетах по формулам (15) и (16) вместо величины $IMAGE42$необходимо использовать $IMAGE71$- радиус Солнца. Тогда:
$IMAGE72$(19)
$IMAGE73$(20)
На рис.3. представлены три зависимости масса-светимость, полученные из экспериментальных данных [3] и на основании расчета по формулам (19) и (20). Из рисунка видно: данные расчета по формуле (19) не согласуются с данными эксперимента, что и следовало ожидать после положительного результата проверки соотношения (18). Вычисления с использованием (20) дают удовлетворительное согласие с экспериментальными данными.
Расчеты по формулам как (15), (16), так и (19), (20) проводились, используя молярную массу вещества $IMAGE74$. Для получения более полной картины, проведем расчет относительных масс звезд по их поверхностной температуре, используя (20) в интервале молярных масс $IMAGE75$. Результаты расчета представлены на рис.4. Все экспериментальные данные, для которых выполнимо (18), попадают в выбранный интервал молярных масс. Отличие угла наклона прямой линии, соединяющей экспериментальные данные, от угла наклона линий, соединяющих соответствующие значения, полученные с помощью (20), может рассматриваться как изменение состава звездного вещества.
$IMAGE76$
$IMAGE77$
Выводы
Как показывают расчеты и их анализ, физическая модель звезд (6)-(12), (20) дает хорошее согласие с экспериментальными данными, демонстрируя тем самым свою жизнеспособность. Из анализа представленной модели следует: изначально тождественные наблюдатели, будучи локализованными возле звезд главной последовательности с различными характеристиками, но удовлетворяющими соотношению (18), будут получать при измерениях масс и радиусов этих звезд одинаковые результаты. Это может связываться только с соответствующим изменением свойств пространства-времени и требует дополнительного рассмотрения. Однако предложенная модель не дает полной физической картины, поскольку выражение для расчета масс звезд (20) содержит поправку $IMAGE78$, природа которой в данной работе не рассматривается. Как показывает предварительный анализ, решение данного вопроса связано с фундаментальными свойствами пространства-времени и затрагивает проблему барионной асимметрии вселенной. Помимо этого, не смотря на то, что из проверенного выражения (3), при определенных условиях, вытекает взаимосвязь таких явлений как тяготение и электромагнитное излучение, требование равенства выражений (6) и (7), опять же в рамках данной работы, нельзя назвать достаточно проработанным и ясным для понимания, что бы составить альтернативу условию механического равновесия вещества звезд [1].
Список литературы
Я.Б. Зельдович, С.И. Блинников, Н.И. Шакура. Физические основы строения и эволюции звезд. - М.: Изд-во МГУ, 1981. – 150 с.
И.С.Шкловский. Звезды: их рождение жизнь и смерть. - М.: Наука, 1984. – 384 с.
Martin V. Zombeck’s. Handbook of Space Astronomy and Astrophysics.: - Cambridge University Press. 1990. – 528 с.
Для подготовки данной работы были использованы материалы с сайта http://www.sciteclibrary.ru