Міністерство освіти і науки України
Приватний вищий навчальний заклад
Європейський університет
Запорізька філія
Реферат
Граничні теореми теорії ймовірностей
з дисципліни: Теорія ймовірностей та математична статистика
Запоріжжя,
2007р.
Теорема Бернуллі. Нехай імовірність появи події А в кожному із п незалежних повторних випробувань дорівнює р, т - число появ події А (частота події) в п випробуваннях. Тоді
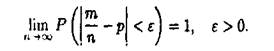
Доведення. Частість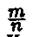 
можна розглядати як невід'ємну випадкову величину 
. Знайдемо її математичне сподівання
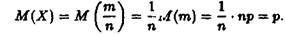
Отже, необхідно оцінити імовірність відхилення випадкової величини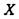 
від її математичного сподівання. Для цього знайдемо дисперсію цієї випадкової величини
$IMAGE6$
За нерівністю Чебишова одержимо
$IMAGE7$
Звідси граничним переходом $IMAGE8$одержуємо (4), що й треба було довести.
Теорема Чебишова. Нехай $IMAGE9$- послідовність попарно незалежних випадкових величин, які задовольняють умовам
$IMAGE10$
для усіх t = 1,2,..., п.
Тоді $IMAGE11$
Доведення. Знайдемо математичне сподівання та дисперсію $IMAGE12$середньої випадкових величин, тобто
$IMAGE13$
$IMAGE14$
Застосуємо для випадкової величини нерівність Чебишова (2)
$IMAGE15$
$IMAGE16$
Границя цієї імовірності при $IMAGE17$ дорівнює одиниці, тобто рівність (5) доведено.
Центральна гранична теорема. Нехай задана послідовність незалежних однаково розподілених випадкових величин
$IMAGE18$ $IMAGE19$
Розглянемо випадкову величину $IMAGE20$Тоді
$IMAGE21$
При $IMAGE22$функція розподілу
$IMAGE23$
тобто сума $IMAGE24$буде розподілена за нормальним законом з математичним сподіванням 0 та дисперсією $IMAGE25$
Для доведення цієї теореми треба знайти границю характеристичної функції, побудованої для нормованої випадкової величини
$IMAGE26$
Наслідок. При $IMAGE27$розподіл суми однаково розподілених випадкових величин мало відрізняється від нормального розподілу.
Теорема Ляпунова. Нехай задана послідовність незалежних випадкових величин $IMAGE28$таких, що
$IMAGE29$
Побудуємо суму випадкових величин $IMAGE30$ Позначимо $IMAGE31$Якщо виконується умова рівномірної малості величин, що утворюють суму
$IMAGE32$
$IMAGE33$то сума $IMAGE34$буде розподіленою нормально з математичним сподіванням $IMAGE35$та дисперсією
Доведення цієї теореми досить складне, але відмітимо, що у випадку, коли $IMAGE36$можна розглядати випадкові величини $IMAGE37$ Величини $IMAGE38$будуть задовольняти умову теореми Ляпунова.
Приклад 2. Скільки додатків треба взяти у теоремі Чебишова, щоб з надійністю 96% і точністю до 0.01 виконувалась наближена рівність
$IMAGE39$
Розв'язок. В цьому прикладі є = 0.01. Щоб одержати надійність 96% згідно формули (6) достатньо підібрати таке п, яке задовольняє нерівність
$IMAGE40$
Зауваження 1. Приклад 2 показує, що навіть у випадку не дуже великих точності та надійності, треба брати значну кількість додатків (п - досить велике число). Це означає, що оцінки, одержані з використанням нерівності (6), - завищені. Більш точні оцінки можна одержати за допомогою теореми Ляпунова.
Список використаної літератури
1. Барковський В.В., Барковська Н.В., Лопатін О.К. теорія ймовірностей та математична статистика. – К.: ЦУЛ, 2002. – 448с.
2. Гмурман В.Е. теория вероятностей и математическая статистика. – М.: Высшая школа, 1980.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1975.
4. Гнеденко Б.В. Курс теории вероятностей. – М.: наука, 1988.
5. Леоненко М.М., Мішура Ю.С. та ін. Теоретико-ймовірностні та статистичні методи в економетриці та фінансовій математиці. – К.: Інформтехніка, 1995.