ФУНКЦІЯ, ЇЇ ГРАНИЦЯ ТА НЕПЕРЕРВНІСТЬ
1. Функція багатьох змінних. Означення та символіка
Нехай задано множину  упорядкованих пар чисел
упорядкованих пар чисел 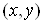 . Якщо кожній парі чисел
. Якщо кожній парі чисел 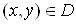 за певним законом відповідає число z, то кажуть, що на множині
за певним законом відповідає число z, то кажуть, що на множині  визначено функцію
визначено функцію 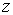 від двох змінних x і $IMAGE6$ і записують $IMAGE7$.
від двох змінних x і $IMAGE6$ і записують $IMAGE7$.
Змінну 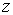 називають залежною змінною (функцією), а змінні x та $IMAGE6$ – незалежними змінними (аргументами).
називають залежною змінною (функцією), а змінні x та $IMAGE6$ – незалежними змінними (аргументами).
Множину пар 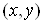 значень x та $IMAGE6$, для яких функція $IMAGE7$ визначена, називають областю визначення цієї функції і позначають $IMAGE13$ або
значень x та $IMAGE6$, для яких функція $IMAGE7$ визначена, називають областю визначення цієї функції і позначають $IMAGE13$ або  .
.
Множину значень 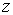 позначають $IMAGE16$або $IMAGE17$.
позначають $IMAGE16$або $IMAGE17$.
Оскільки кожній упорядкованій парі чисел 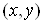 відповідає в прямокутній системі координат $IMAGE19$ єдина точка $IMAGE20$ площини, що те саме, точка двовимірного простору $IMAGE21$, і, навпаки, кожній точці $IMAGE20$ площини відповідає єдина упорядкована пара чисел
відповідає в прямокутній системі координат $IMAGE19$ єдина точка $IMAGE20$ площини, що те саме, точка двовимірного простору $IMAGE21$, і, навпаки, кожній точці $IMAGE20$ площини відповідає єдина упорядкована пара чисел 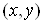 , то функцію $IMAGE7$, де
, то функцію $IMAGE7$, де 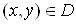 , можна розглядати як функцію точки $IMAGE26$ і замість $IMAGE7$ писати $IMAGE28$. Областю визначення $IMAGE29$ функції у цьому випадку є деяка множина точок площини $IMAGE19$. Зокрема, областю визначення функції може бути вся площина, або частина площини, обмежена певними лініями.
, можна розглядати як функцію точки $IMAGE26$ і замість $IMAGE7$ писати $IMAGE28$. Областю визначення $IMAGE29$ функції у цьому випадку є деяка множина точок площини $IMAGE19$. Зокрема, областю визначення функції може бути вся площина, або частина площини, обмежена певними лініями.
Значення функції $IMAGE7$ в точці $IMAGE32$ позначають $IMAGE33$ або $IMAGE34$, або $IMAGE35$.
Лінію, що обмежує область  , називають межею області визначення. Точки області, які не лежать на її межі, називаються внутрішніми. Область, яка містить одні внутрішні точки називається відкритою. Якщо ж до області визначення належать і всі точки межі, то така область називається замкненою.
, називають межею області визначення. Точки області, які не лежать на її межі, називаються внутрішніми. Область, яка містить одні внутрішні точки називається відкритою. Якщо ж до області визначення належать і всі точки межі, то така область називається замкненою.
Функція двох змінних, як і функція однієї змінної, може бути задана різними способами. Користуватимемося, як правило, аналітичним способом, коли функція задається за допомогою формули. Областю визначення такої функції вважається множина всіх тих точок площини, для яких задана формула має зміст.
Приклади
Знайти область визначення  функції
функції
а) $IMAGE38$;
б) $IMAGE39$.
Розв’язання
а) Область $IMAGE40$ даної функції – множина тих точок $IMAGE41$, для яких вираз $IMAGE42$має зміст, тобто множина точок, для яких $IMAGE43$. Це означає, що функція визначена в точках, які знаходяться всередині кола $IMAGE44$ і на його межі, оскільки всі точки, які знаходяться зовні кола задовольняють умову $IMAGE45$.
б) Область визначення  цієї функції визначається з нерівності $IMAGE47$, тобто $IMAGE48$.
цієї функції визначається з нерівності $IMAGE47$, тобто $IMAGE48$.
Точки площини $IMAGE19$, координати яких задовольняють цю нерівність, розташовані під прямою $IMAGE50$, причому точки, які розташовані на цій прямій не належать області  .
.
Функцію двох змінних можна зобразити графічно у вигляді деякої поверхні. Дійсно, нехай функція $IMAGE7$ визначена в області  . Кожній точці $IMAGE54$ відповідає певне значення функції $IMAGE7$.
. Кожній точці $IMAGE54$ відповідає певне значення функції $IMAGE7$.
Графіком функції $IMAGE7$ у прямокутній системі $IMAGE57$ називається геометричне місце точок $IMAGE58$, проекції яких $IMAGE59$ належать області  . Це геометричне місце точок утворює в тривимірному просторі $IMAGE61$ певну поверхню (рис.1), проекцією якої на площину $IMAGE19$ є множина
. Це геометричне місце точок утворює в тривимірному просторі $IMAGE61$ певну поверхню (рис.1), проекцією якої на площину $IMAGE19$ є множина  .
.
$IMAGE64$
Рисунок 1 – Поверхня у тривимірному просторі
Приклади
а) Графіком функції $IMAGE65$, як відомо з аналітичної геометрії, є параболоїд обертання.
б) Графіком функції $IMAGE66$ є гіперболічний параболоїд.
При побудові графіків функцій двох змінних часто стикаємося із значними труднощами. В зв’язку з цим для зображення функції двох змінних користуються методом перерізів, який полягає у тому, що поверхню $IMAGE7$перетинають площинами $IMAGE68$ та $IMAGE69$ і за графіками кривих $IMAGE70$ та $IMAGE71$визначають графік функції $IMAGE7$.
Можна фіксувати не x чи $IMAGE6$, а саму функцію 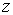 , тобто перетинати дану поверхню площинами $IMAGE75$, де c – довільне число, взяте з множини $IMAGE16$ значень даної функції. Таким чином отримаємо криву $IMAGE77$, яку називають
, тобто перетинати дану поверхню площинами $IMAGE75$, де c – довільне число, взяте з множини $IMAGE16$ значень даної функції. Таким чином отримаємо криву $IMAGE77$, яку називають
лінією рівня функції. Інакше кажучи, лінія рівня на площині $IMAGE19$ – це проекція кривої, яка утворюється при перетині поверхні $IMAGE7$ площиною $IMAGE75$. Якщо побудувати лінії рівня для різних значень c, можна отримати уявлення про графік функції двох змінних.
Приклад
Знайти лінії рівня функції $IMAGE81$.
Розв’язання
Лініями рівня даної функції є кола з радіусом $IMAGE82$ (рис. 2). Зокрема, якщо $IMAGE83$, то отримуємо коло $IMAGE84$.
$IMAGE85$
Рисунок 2 – Лінії рівня функції $IMAGE81$
Поняття функції двох змінних узагальнимо на випадок трьох і більшого числа незалежних змінних.
Нехай  – деяка множина упорядкованих трійок $IMAGE88$дійсних чисел, тобто точок $IMAGE89$тривимірного простору $IMAGE61$.
– деяка множина упорядкованих трійок $IMAGE88$дійсних чисел, тобто точок $IMAGE89$тривимірного простору $IMAGE61$.
Якщо кожній точці $IMAGE91$ за певним законом відповідає єдине число $IMAGE92$, то кажуть, що на множині  визначено функцію u від трьох змінних $IMAGE94$ і
визначено функцію u від трьох змінних $IMAGE94$ і 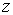 та записують $IMAGE96$ або $IMAGE97$.
та записують $IMAGE96$ або $IMAGE97$.
При цьому змінна $IMAGE92$ називається залежною змінною (функцією), $IMAGE99$– незалежними змінними (аргументами), множина $IMAGE100$ – областю визначення функції.
Область визначення функції трьох змінних можна геометрично зобразити у вигляді деякої частини тривимірного простору.
Поверхнею рівня функції $IMAGE96$ називають множину всіх точок $IMAGE102$, для яких задана функція набуває одне й те саме значення $IMAGE103$: $IMAGE104$.
Приклади
Областю визначення функції
$IMAGE105$
є куля радіуса $IMAGE106$ з центром у початку координат. Це замкнена область, оскільки їй належать точки сфери $IMAGE107$ – межі області.
2. Поверхні рівня функції $IMAGE108$ визначаються рівнянням $IMAGE109$,
· Якщо $IMAGE83$, то отримуємо $IMAGE111$ – конус;
· якщо $IMAGE112$, то $IMAGE109$ – сім’я однопорожнинних гіперболоїдів;
· якщо $IMAGE114$, то $IMAGE109$ – сім’я двопорожнинних гіперболоїдів.
Лінії та поверхні рівня досить часто зустрічаються на практиці. Зокрема, ізотерми та ізобари є важливими даними для прогнозу погоди.
Якщо число n незалежних змінних більше трьох, то їх часто позначають однією буквою, але з різними індексами: $IMAGE116$.
Функцію u від цих незалежних змінних можна визначити так. Нехай задано множину  упорядкованих систем $IMAGE118$з n чисел $IMAGE119$ або, що те саме, множину точок $IMAGE120$ n– вимірного простору $IMAGE121$.
упорядкованих систем $IMAGE118$з n чисел $IMAGE119$ або, що те саме, множину точок $IMAGE120$ n– вимірного простору $IMAGE121$.
Якщо кожній точці $IMAGE122$за певним законом відповідає єдине число u, то кажуть, що на множині  визначено функцію u від n змінних: $IMAGE116$і записують
визначено функцію u від n змінних: $IMAGE116$і записують
$IMAGE125$або $IMAGE97$, $IMAGE127$.
Надалі розглядатимемо функції двох змінних, оскільки результати для функцій двох змінних легко за аналогією узагальнити на випадок більшого числа змінних.
2. Границя функції багатьох змінних
функція формула неперервність змінна
Введемо поняття $IMAGE128$ – околу заданої точки $IMAGE129$і поняття збіжної послідовності точок площини.
Множина всіх точок $IMAGE130$, координати яких задовольняють нерівність
$IMAGE131$,
де $IMAGE132$ – відстань від точки $IMAGE26$ до $IMAGE134$, називається $IMAGE128$-околом точки $IMAGE129$.
Розглянемо послідовність точок $IMAGE137$, $IMAGE138$, …, $IMAGE139$, яку позначимо символом $IMAGE140$. Послідовність точок $IMAGE140$ називається збіжною до точки $IMAGE134$, якщо для довільного числа $IMAGE143$ існує номер $IMAGE144$такий, що при $IMAGE145$ виконується нерівність $IMAGE146$. При цьому точку $IMAGE134$ називають границею послідовності $IMAGE140$ і записують так:
$IMAGE149$або $IMAGE150$ при $IMAGE151$.
Якщо $IMAGE152$ при $IMAGE151$, то, очевидно, $IMAGE154$, $IMAGE155$ при $IMAGE151$.
Тепер розглянемо границю функції двох змінних. Її означення аналогічне означенню границі функції однієї змінної. Нехай функція $IMAGE7$ задана в деякій області  і точка $IMAGE159$або $IMAGE160$, але має таку властивість, що в довільному $IMAGE128$-околі цієї точки міститься хоча б одна точка множини
і точка $IMAGE159$або $IMAGE160$, але має таку властивість, що в довільному $IMAGE128$-околі цієї точки міститься хоча б одна точка множини  , відмінна від $IMAGE134$. Число $IMAGE164$ називається границею функції $IMAGE28$в точці $IMAGE134$, якщо для довільної, збіжної до $IMAGE134$ послідовності точок $IMAGE168$, відповідна послідовність значень функції $IMAGE169$збігається до числа $IMAGE164$. При цьому пишуть:
, відмінна від $IMAGE134$. Число $IMAGE164$ називається границею функції $IMAGE28$в точці $IMAGE134$, якщо для довільної, збіжної до $IMAGE134$ послідовності точок $IMAGE168$, відповідна послідовність значень функції $IMAGE169$збігається до числа $IMAGE164$. При цьому пишуть:
$IMAGE171$, або $IMAGE172$.
Наведене означення границі функції називають означенням за Гейне або означенням „на мові послідовностей”.
Дамо еквівалентне означення границі функції за Коші або означення „на мові $IMAGE173$”. Число $IMAGE164$ називається границею функції $IMAGE28$в точці $IMAGE134$, якщо для кожного числа $IMAGE143$ знайдеться число $IMAGE178$ таке, що для всіх точок $IMAGE179$, які задовольняють умову $IMAGE180$, виконується нерівність $IMAGE181$.
Користуючись означенням границі функції двох змінних, можна перенести основні теореми про границі для функції однієї змінної на функції двох змінних. Наприклад, правильне таке твердження.
Теорема. Нехай функції $IMAGE182$ і $IMAGE183$ визначені на одній і тій самій
множині  і мають в точці $IMAGE134$ границі $IMAGE186$ і $IMAGE187$.
і мають в точці $IMAGE134$ границі $IMAGE186$ і $IMAGE187$.
Тоді функції $IMAGE188$, мають в
точці $IMAGE134$ границі, які відповідно дорівнюють $IMAGE190$.
Функція $IMAGE28$ називається нескінченно малою в точці $IMAGE134$ (або при $IMAGE193$), якщо $IMAGE194$.
Якщо функція $IMAGE28$ має в точці $IMAGE26$ границю, яка дорівнює $IMAGE164$, то
функція $IMAGE198$ є нескінченно малою в точці $IMAGE134$, тому що $IMAGE200$. Звідси випливає, що функція $IMAGE182$в околі точки $IMAGE134$ відрізняється від границі $IMAGE164$ на нескінченно малу функцію.
Приклади
Знайти границі:
а) $IMAGE204$
б) $IMAGE205$
Розв’язання
а) Якщо $IMAGE206$, то $IMAGE207$, тому
$IMAGE208$.
б) Умова $IMAGE209$ еквівалентна умові $IMAGE210$.
Оскільки $IMAGE211$,
То
$IMAGE212$
і, отже,
$IMAGE213$
Означення границі функції $IMAGE214$ змінних при $IMAGE215$ аналогічне означенням границі при $IMAGE216$ , якщо в $IMAGE214$-вимірному просторі ввести таке поняття $IMAGE128$-околу: $IMAGE128$-околом точки $IMAGE220$ називається множина всіх точок $IMAGE120$, координати яких задовольняють нерівності
$IMAGE222$.
Зокрема, у тривимірному просторі $IMAGE61$ $IMAGE128$-околом точки $IMAGE225$ є множина всіх внутрішніх точок $IMAGE89$ кулі з центром у точці $IMAGE134$ радіуса $IMAGE128$.
3. Неперервність функції багатьох змінних
Поняття неперервної функції багатьох змінних вводиться за допомогою поняття границі.
Нехай функція $IMAGE28$ визначена на множині  , точка $IMAGE231$ і довільний $IMAGE128$-окіл точки $IMAGE134$ містить точки множини
, точка $IMAGE231$ і довільний $IMAGE128$-окіл точки $IMAGE134$ містить точки множини  .
.
Функція $IMAGE28$ називається неперервною в точці $IMAGE134$, якщо
$IMAGE237$.(1)
У випадку функції двох змінних рівність (1) означає, що коли точка $IMAGE20$, залишаючись в області визначення  функції $IMAGE7$, наближається до точки $IMAGE32$, то відповідна апліката $IMAGE182$поверхні, яка є графіком заданої функції, прямує до аплікати $IMAGE243$.
функції $IMAGE7$, наближається до точки $IMAGE32$, то відповідна апліката $IMAGE182$поверхні, яка є графіком заданої функції, прямує до аплікати $IMAGE243$.
Точки, в яких функція неперервна, називаються точками неперервності, а точки, в яких неперервність порушується – точками розриву цієї функції.
Приклад
Неперервність функції
$IMAGE244$
в довільній точці $IMAGE32$, крім точки $IMAGE246$, випливає із неперервності многочлена, синуса, квадратного кореня і умови $IMAGE247$; неперервність $IMAGE248$ в точці $IMAGE134$(0;0) випливає із рівності
$IMAGE250$(п. 2).
Умові (1) неперервності можна надати іншого вигляду. Позначимо
$IMAGE251$, $IMAGE252$, $IMAGE253$.
Величини $IMAGE254$, $IMAGE255$ називають приростами аргументів x і $IMAGE6$, а $IMAGE257$– повним приростом функції $IMAGE248$ в точці $IMAGE259$. З рівності (1) отримуємо:
$IMAGE260$
$IMAGE261$. (2)
Рівність (2) дає ще одне означення неперервності.
Функція $IMAGE248$ називається неперервною в точці $IMAGE32$, якщо повний приріст її в цій точці прямує до нуля, коли прирости її аргументів x та $IMAGE6$прямують до нуля.
Функція $IMAGE248$ називається неперервною на множині  , якщо вона неперервна в кожній точці $IMAGE59$ цієї множини.
, якщо вона неперервна в кожній точці $IMAGE59$ цієї множини.
Приклад
Функція $IMAGE65$ неперервна на всій площині $IMAGE19$, оскільки повний приріст цієї функції в довільній точці $IMAGE259$ має вигляд
$IMAGE271$
$IMAGE272$.
Використовуючи поняття неперервності функції кількох змінних і відповідні теореми про границі, можна довести, що арифметичні операції над неперервними функціями і побудова складеної функції з неперервних фу