Зміст
Введення
Глава I. Розвиток геометрії
1.1 Історія геометрії
1.2 Постулати Евкліда
1.3 Аксіоматика Гильберта
1.4 Інші системи аксіом геометрії
Глава II. Неевклідові геометрії в системі Вейля
2.1 Елементи сферичної геометрії
2.2 Еліптична геометрія на площині
2.3 Геометрія Лобачевского в системі Вейля
2.4 Різні моделі площини Лобачевского. Незалежність 5-го постулату Евкліда від інших аксіом Гильберта
Висновок
Список літератури
Введення
Будь-яка теорія сучасної науки вважається єдино вірної, поки не створена наступна. Це своєрідна аксіома розвитку науки.
Цей факт багаторазово підтверджувався. Фізика Ньютона переросла в релятивістську фізику, а та у квантову. Теорія флогістону стала хімією, а самозародження мишей із бруду обернулося біологією. Така доля всіх наук, і не можна сказати, що сьогоднішнє відкриття через двадцять років не виявиться грандіозною помилкою. Але це теж нормально - ще Ломоносов говорив: «Алхімія - мати хімії: дочка не винувата, що її мати дурнувата».
Доля ця не обійшла й геометрію. Традиційна Евклідова геометрія переросла в неевклідову, геометрію Лобачевского. Саме цьому розділу математики, його історії й особливостям і присвячений цей проект.
У даній дипломній роботі я хочу показати, що крім геометрії, що вивчають у школі (Геометрії Евкліда або вживаної геометрії), існує ще одна геометрія, геометрія Лобачевского. Ця геометрія істотно відрізняється від евклідової, наприклад, у ній затверджується, що через дану крапку можна провести нескінченно багато прямих, паралельних даній прямій, що сума кутів трикутника менше 180?? У геометрії Лобачевского не існує прямокутників, подібних трикутників і так далі.
Я вибрав дану тему з кількох причин: теорія геометрії Лобачевского допомагає глянути по-іншому на навколишній нас мир, це цікавий, незвичайний і прогресивний розділ сучасної геометрії, вона дає матеріал для міркувань - у ній не все просто, не все ясно з першого погляду, щоб неї зрозуміти, потрібно мати фантазію й просторову уяву. Ситуація з геометрією Лобачевского й геометрією Евкліда багато в чому схожа на ситуацію з Теорією відносності Ейнштейна й класичною фізикою. Геометрія Лобачевского й Ейнштейна це прогресивні взаємозалежні теорії, що виконуються на величезних величинах і відстанях, і, що залишаються вірними на наближеннях до нуля. У просторовій моделі використовується не звичайна евклідова площина, а скривлений простір, на якому вірна теорія Лобачевского.
евклідова геометрія аксіома площа
Глава I. Розвиток геометрії
1.1 Історія геометрії
Геометрія - це одна з найдавніших наук. Досліджувати різні просторові форми здавна спонукувало людей їхня практична діяльність. Давньогрецький учений Едем Родоський в IV столітті до нашої ери писала: «Геометрія була відкрита єгиптянами, і виникла при вимірі Землі. Цей вимір було їм необхідно внаслідок розлиття ріки Нил, що постійно змивала границі. Немає нічого дивного, що ця наука, як і інші, виникла з потреби людини».
Уважається, що геометрія почалася в так званої Їонийської школі. Її засновником уважається Фалес Милетський (640-540 (546?) рр. до н.е.). Він уважався одним із семи мудреців Греції, першим математиком, астрономом і філософом. Він довів, що кути при підставі рівнобедреного трикутника рівні, що вертикальні кути рівні, що діаметр ділить окружність навпіл і ще множина теорем. Пророкування затьмарення сонця в 585 році також приписується йому.
Величезний імпульс розвитку цій школі дав Піфагор (569-470 р. до н.е.). В основному про його особисті якості пишуть те ж саме, що й про Фалесе. Але до цього ще можна додати титул чемпіона з боксу на олімпійських іграх - звання, серед математиків рідке.
Незважаючи на всі його досягнення, думку сучасників добре виразив Геракліт: «Багато знання без розуму». Що ж, це було цілком заслужене: Піфагор засекречував відкриття й приписував собі роботи учнів. Піфагор також змушував своїх вихованців виконувати цілий звід дуже дивних правил: наприклад, не доторкатися до білого півня.
Але факт є факт - і одна з теорем Піфагора тепер відома кожному – це теорема про рівність квадрата гіпотенузи сумі квадратів катетів. Ця теорема настільки популярна у світі математиків, що одних тільки доказів нагромадилося 39 штук.
Платон (428-348) знаменитий введенням принципу дедуктивності в математику, або принципу розвитку від простого до складного. Він також знаменитий постановкою трьох задач на побудову. Використовуючи тільки циркуль і лінійку, треба було:
Розділити кут на три частини (задача про трисекцію кута).
Побудувати квадрат, рівний по площі даному колу (задача про квадратуру кола).
Побудувати куб, рівний по об'єму даному (задача про подвоєння куба).
Не можливість вирішення цих задач була доведена тільки в 19 столітті, але перед цим вони встигли викликати справжню буру: наприклад, задача №2 викликала появу інтегрального вирахування.
Багато первісних геометричних відомостей одержали також шумеро-вавилонські, китайські й інші вчені найдавніших часів. Установлювалися вони сНачало тільки досвідченим шляхом, без логічних доказів.
Як наука, геометрія вперше сформувалася в Древній Греції, коли геометричні закономірності й залежності, знайдені раніше досвідченим шляхом, були наведені в належну систему й доведені.
Закінчився розвиток традиційної геометрії Евклідом. В III столітті до нашої ери грецький учений привело в систему відомі йому геометричні відомості у великому творі «Начало».
Його книга «Начало» тільки до 1880 року витримала 460 видань, поступившись тільки Біблії. Спосіб побудови став єдино вірним для всіх наукових праць: Перерахування основних, природних понять (Перерахування основних аксіом (Перерахування основних визначень (Формулювання теорем (тверджень) і їхній доказ.
Метод доказу від противного – теж його заслуга. Він же сформулював п'ять постулатів геометрії:
Через дві крапки можна провести одну й тільки одну пряму.
Пряма триває нескінченно.
З будь-якого центра можна провести окружність будь-яким радіусом.
Всі прямі кути рівні між собою.
П'ятий постулат є своєрідним філософським каменем геометрії.
Неевклідова геометрія з'явилася внаслідок довгих спроб довести V постулат Евкліда, аксіому паралельності. Ця геометрія багато в чому дивна, незвичайна й багато в чому не відповідає нашим звичним уявленням про реальний світ. Але в логічному відношенні дана геометрія не уступає геометрії Евкліда.
1.2 Постулати Евкліда
Евклід - автор першого логічної побудови, що дійшло до нас строгого, геометрії. У ньому виклад настільки бездоганно для свого часу, що протягом двох тисяч років з моменту появи його праці «Начало» воно було єдиним керівництвом для вивчаючу геометрію.
«Начало» складаються з 13 книг, присвячених геометрії й арифметиці в геометричному викладі.
Кожна книга «Начало» починається визначенням понять, які зустрічаються вперше. Так, наприклад, першій книзі подані 23 визначення. Зокрема,
Визначення 1. Крапка є те, що не має частин.
Визначення 2. Лінія є довжини без ширини
Визначення 3. Границі лінії суть крапки.
Слідом за визначеннями Евклід приводить постулати й аксіоми, тобто твердження, прийняті без доказу.
Постулати
I. Потрібно, щоб від кожної крапки до всякої іншої крапки можна було провести пряму лінію.
II . І щоб кожну пряму можна було невиразно продовжити.
III. І щоб з будь-якого центра можна було описати окружність будь-яким радіусом.
IV. І щоб всі прямі кути були рівні.
V. І щоб щораз, коли пряма при перетинанні із двома іншими прямими утворить із ними однобічні внутрішні кути, сума яких менше двох прямих, ці прямі перетиналися з тієї сторони, з якої ця сума менше двох прямих.
Аксіоми
I. Рівні порізно третьому рівні між собою.
II. І якщо до них додамо рівні, то одержимо рівні.
III. І якщо від рівних віднімемо рівні, то одержимо рівні.
IV. І якщо до нерівного додамо рівні, то одержимо нерівні.
V. І якщо подвоїмо рівні, то одержимо рівні.
VI. І половини рівних рівні між собою.
VII. І сумісні рівні.
VIII. І ціле більше частини.
IX. І дві прямі не можуть містити простори.
Іноді IV і V постулати відносять до числа аксіом. Тому п'ятий постулат іноді називають XI аксіомою. По якому принципі одні твердження ставляться до постулатів, а інші до аксіом, невідомо.
Ніхто не сумнівався в істинності постулатів Евкліда, що стосується й V постулату. Тим часом уже зі стародавності саме постулат про паралельні залучив до себе особлива увага ряду геометрів, що вважали неприродним приміщення його серед постулатів. Імовірно, це було пов'язане з відносно меншою очевидністю й наочністю V постулату: у неявному виді він припускає досяжність будь-яких, як завгодно далеких частин площини, виражаючи властивість, що виявляється тільки при нескінченному продовженні прямих.
Можливо, що вже сам Евклід намагався довести постулат про паралельні. На користь цього говорить та обставина, що перші 28 пропозицій «Начало» не опираються на V постулат. Евклід як би намагався відсунути застосування цього постулату доти, поки використання його не стане настійно необхідним.
Одні математики намагалися довести постулат про паралельний, застосовуючи тільки інші постулати й ті теореми, які можна вивести з останніх, не використовуючи сам V постулат. Всі такі спроби виявилися невдалими. Їхній загальний недолік у тім, що в доказі неявно застосовувалося яке-небудь припущення, рівносильне доказуваному постулату.
Інші пропонували по-новому визначити паралельні прямі або ж замінити V постулат яким-небудь, на їхню думку, більше очевидною пропозицією. Так, наприклад, в XI столітті Омар Хайям увело замість V постулату «принцип», відповідно до якого дві лежачі в одній площині збіжні прямі перетинаються й не можуть розходитися в напрямку сходження. За допомогою цього принципу Хайям доводить, що в чотирикутнику ABCD, у якому кути при підставі А и В - прямі й сторони АС, ВD рівні, кути С и D так само прямі, а із цієї пропозиції про існування прямокутника виводиться V постулат. Міркування Хайяма одержали оригінальний розвиток в XIII столітті в Насиредина ат-туси, роботи якого у свою чергу стимулювали дослідження Д. Валлиса. В 1663 році Валлис довів постулат про паралельний, виходячи з явного допущення, що для кожної фігури існує подібна їй фігура довільної величини. Це допущення він уважав, що випливає з істоти просторових відносин.
З логічної точки зору результати Хайяма або Валлиса лише виявляли рівносиль V постулату й деяких інших пропозицій геометрії. Так, Хайям, по суті, установив еквівалентність постулату й пропозиції про суму кутів трикутника, а Валлис показав, що не тільки з V постулату можна вивести вчення про подобу, але й обернено - їх Евклідова вчення про подобу треба V постулат.
Один з підбадьорюючих способів підходу до доказу п'ятого постулату, яким користувалися багато геометрів XVIII і першої половини XIX століть, полягає в тому, що п'ятий постулат заміняється його запереченням або яким-небудь твердженням, еквівалентним запереченню. Опираючись на змінену в такий спосіб систему постулатів і аксіом, доводяться всілякі пропозиції, логічно з її що випливають. Якщо п'ятий постулат дійсно випливає з інших постулатів і аксіом, то змінена зазначеним образом система постулатів мі аксіом суперечлива. Тому рано або пізно ми прийдемо у двом взаємно, що виключають висновкам. Цим і буде доведений п'ятий постулат.
Саме таким шляхом намагалися довести п'ятий постулат Д. Саккери (1667-1733), И. Г. Ламберт (1728-1777) і А.М. Лежандр (1752-1833).
Дослідження Саккери були опубліковані в 1733 році за назвою «Евклід, очищений від усяких плям, або досвід, що встановлює найперші принципи універсальної геометрії».
Саккери виходив з розгляду чотирикутника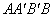 
із двома прямими кутами при підставі 
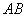й із двома рівними бічними сторонам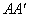и 
й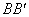 
. Із симетрії фігури щодо перпендикуляра 
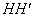до середини підстави 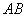треба, що кути при вершинах $IMAGE7$ і $IMAGE8$ рівні. Якщо прийняти п'ятий постулат і, отже, Евклідову теорію паралельних, то можна встановити, що кути $IMAGE7$ й $IMAGE8$ прямі й 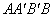- прямокутник. Обернено, як доводить Саккери, якщо хоча б в одному чотирикутнику зазначеного виду кути при верхній підставі виявляться прямими, то буде мати місце Евклідов постулат про паралельні. Бажаючи довести цей постулат Саккери робить три можливих припущення: або кути $IMAGE7$ й $IMAGE8$ прямі, або тупі, або гострі (гіпотези прямого, гострого й тупого кута). Для доказу п'ятого постулату необхідно спростувати гіпотези гострого й тупого кута. Зовсім точними міркуваннями Саккери приводить до протиріччя гіпотезу тупого кута. Слідом за тим, прийнявши гіпотезу гострого кута, він виводить досить що далеко йдуть її наслідки для того, щоб і тут одержати протиріччя. Розвиваючи ці наслідки Саккери будує складну геометричну систему, не містячи про протиріччя тільки тому, що отримані їм висновки не відповідають звичним уявленням про розташування прямих. У результаті він «знаходить» логічне протиріччя, але в результаті обчислювальної помилки.
Ідеї Ламберта, розвинені їм у творі «теорія паралельних ліній» (1766р.), близько примикають до міркувань Саккери.
Він розглядає чотирикутник із трьома прямими кутами. Щодо четвертого кута так само виникають три гіпотези: цей кут прямий, тупий або гострий. Довівши еквівалентність п'ятого постулату гіпотезі прямого кута й зві