Содержание
Введение
§1. Линейные преобразования
§2. Индексные обозначения
§3. Общее определение тензоров
§4. Скалярное произведение и метрический тензор
§5. Действия с тензорами
§6. Поднятие и опускание индексов
§7. Тензоры в криволинейных координатах
§8. Примеры вычислений
Заключение
Литература
Введение
Возникновение тензорного исчисления было подготовлено в 19 веке развитием теории алгебраических форм, с одной стороны, и теории квадратичных дифференциальных форм - с другой. Исследования в области теории дифференциальных квадратичных форм были непосредственно связаны с дифференциальной геометрией: с геометрией поверхностей (К. Гаусс) и с геометрией многомерного метрического пространства (Б. Риман). Современную форму тензорному исчислению придал итальянский математик Г. Риччи-Курбастро, поэтому тензорное исчисление иногда называется исчислением Риччи. Идеи Риччи-Курбастро первоначально не получили широкого распространения. Внимание к ним возросло после появления (1915-16) общей теории относительности А. Эйнштейна, математическая часть которой целиком основана на тензорном исчислении.
Тензор (от лат. tensus - напряжённый, натянутый), математический термин, появившийся в середине 19 века и с тех пор применяющийся в двух различных смыслах. Наибольшее распространение термин «тензор» получил в современном тензорном исчислении, где это название присваивается особого рода величинам, преобразующимся по особому закону. В механике, особенно в теории упругости, термин «тензор» широко применяется как синоним симметрического аффинора, то есть линейного оператора F, преобразующего вектор х в вектор Fх, и симметрического в том смысле, что скалярное произведение уFх не меняется при перестановке векторов х и у. Здесь термин был первоначально связан с малыми растяжениями (и сжатиями), возникающими при упругой деформации (откуда и название «тензор»), а затем перенесён в другие области механики. Так появились тензор деформации, тензор напряжения, тензор инерции и др.
§1. Линейные преобразования
Пусть переменные 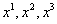 преобразуются в новые
преобразуются в новые 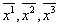 с помощью линейного преобразования
с помощью линейного преобразования

где 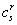 - константы (все индексы пробегают значения 1, 2, 3..., n независимо друг от друга.). Применяя условие о суммировании, можем записать эту систему уравнений в виде
- константы (все индексы пробегают значения 1, 2, 3..., n независимо друг от друга.). Применяя условие о суммировании, можем записать эту систему уравнений в виде
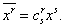 (1.1)
(1.1)
Мы предполагаем, что определитель преобразования $IMAGE6$ не равен нулю. Пусть $IMAGE7$ является алгебраическим дополнением элемента 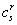 в определителе c деленным на величину $IMAGE9$( $IMAGE9$- обратная матрица). Тогда
в определителе c деленным на величину $IMAGE9$( $IMAGE9$- обратная матрица). Тогда
$IMAGE11$ (1.2)
и мы можем разрешить систему уравнений (1.1) относительно x
$IMAGE12$ (1.3)
Это показывает, что данное преобразование обратимо.
Кроме того, если $IMAGE13$ мы имеем
$IMAGE14$
т. е. тождественное преобразование.
Если перейти сначала от переменных $IMAGE15$к $IMAGE16$по (1.1), а затем от переменных $IMAGE16$к $IMAGE18$при помощи преобразования
$IMAGE19$
то мы видим, что переход от первоначальных переменных $IMAGE15$ к $IMAGE18$определяется формулой
$IMAGE22$
где
$IMAGE23$
Это преобразование, следовательно, также линейное.
Говорят, что совокупность преобразований образует группу, когда она удовлетворяет следующим условиям: 1) если преобразования от $IMAGE15$к $IMAGE16$ и от $IMAGE16$к $IMAGE18$принадлежат данной совокупности, то преобразование от $IMAGE15$к $IMAGE18$ также принадлежат к ней; 2) совокупность преобразования содержит тождественное и обратное преобразования.
Таким образом, совокупность линейных преобразований образует группу.
§ 2. Индексные обозначения
Если нам дана совокупность трех независимых переменных, то они могут быть обозначены тремя различными буквами, например x,y,z, но мы считаем более удобным обозначать переменные данной совокупности одной и той же буквой, различая их посредством индексов. Таким образом, мы можем записать три переменные в виде $IMAGE30$, или в более компактной форме:
$IMAGE31$ (2.1)
Здесь мы написали индекс внизу, но в равной мере мы могли бы использовать вместо этого верхний значок, так что переменные были бы записаны в виде 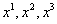 или
или
$IMAGE33$ (2.2)
Однородная линейная функция переменных обычно записывается в виде
$IMAGE34$ (2.3)
где $IMAGE35$ - константы. Таким образом, коэффициенты линейной формы могут быть записаны в виде
$IMAGE36$
Объекты, которые, подобно $IMAGE15$и $IMAGE38$, зависят только от одного индекса, называются объектами первого порядка, а отдельные буквы с индексами 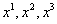 и $IMAGE35$ называются элементами или составляющими объекта. Объекты первого порядка, имеющие три составляющие, назовем трехмерными. Имеются два типа объектов первого порядка, а именно те, у которых индекс вверху, и те, у которых индекс внизу; следовательно, все объекты первого порядка принадлежат к одному из двух типов
и $IMAGE35$ называются элементами или составляющими объекта. Объекты первого порядка, имеющие три составляющие, назовем трехмерными. Имеются два типа объектов первого порядка, а именно те, у которых индекс вверху, и те, у которых индекс внизу; следовательно, все объекты первого порядка принадлежат к одному из двух типов
$IMAGE41$ (2.4)
С другой стороны, однородная квадратичная функция трех переменных имеет вид
$IMAGE42$ (2.5)
где атп - константы. Мы видим, что коэффициенты квадратичной формы зависят от двух индексов и записываются так:
$IMAGE43$
Составляющие этого объекта преобразуются следующим образом:
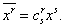
Следовательно, эта формула дает один из способов, с помощью которого может быть преобразован объект первого порядка. Любой объект, составляющие которого преобразуются по этому закону, называется контравариантным вектором. Таким образом, есть контравариантный вектор, если при линейном преобразовании переменных (1.1) его преобразованные составляющие определяются формулами
$IMAGE45$ (2.6)
Имеется и другой способ преобразования элементов объекта первого порядка. Мы уже видели, что коэффициенты линейной формы переменных x также образуют объект первого порядка. Таким образом, коэффициенты линейной формы $IMAGE46$ являются составляющими объекта $IMAGE38$. Предположим, что составляющие $IMAGE38$ преобразуются таким образом, что линейная форма $IMAGE46$ остается инвариантной относительно преобразования переменных (1.1). Если мы обозначим через $IMAGE50$новые составляющие объекта $IMAGE38$ (после преобразования), то получим
$IMAGE52$,
так как эта линейная форма есть инвариант. Тогда из (1.3) следует
$IMAGE53$
Поскольку немой индекс может быть обозначен любой буквой, то эту систему уравнений можно записать в виде
$IMAGE54$
Если это соотношение справедливо для всех значений переменных $IMAGE15$, то должно выполняться равенство
$IMAGE56$ (2.7)
Это преобразование, очевидно, отлично от преобразования, задаваемого формулой (2.6). Объект первого порядка, составляющие которого преобразуются по этому закону, называется ковариантным вектором.
Таким образом, у нас есть два типа тензоров первого порядка, и мы условимся различать их с помощью положения индекса. Если - тензор контравариантен, мы используем верхний индекс, если же он ковариантен, то нижний. Другими словами, верхний индекс обозначает контравариантностъ, а нижний индекс — ковариантность.
Объекты, которые зависят от двух индексов, называются объектами второго порядка. Из того, что индексы бывают верхние и нижние, следует, что объекты второго порядка могут быть трех типов:
$IMAGE57$ (2.8)
Легко видеть, что в этом случае каждый объект имеет 9 составляющих.
Аналогично можно получить объекты третьего порядка, которые будут зависеть от трех индексов и могут принадлежать к любому из четырех типов:
$IMAGE58$ (2.9)
Здесь каждый объект содержит $IMAGE59$или 27 составляющих. Мы можем продолжать это построение и получить объекты любого порядка.
Для законченности этой последовательности мы назовем объект а, не имеющий индексов, объектом нулевого порядка. Если этот объект имеет одно и то же значение и в новых переменных $IMAGE16$ и в старых переменных $IMAGE15$, то он называется скаляром, или инвариантом. Следовательно, если а есть инвариант, то
$IMAGE62$, (2.10)
где $IMAGE63$ есть значение данного объекта в новых переменных.
Мы взяли число измерений равным трем лишь для определенности. Все, что было сказано выше, применимо также к любому числу измерений, если условиться, что число значений, пробегаемых индексом, равно числу измерений. Например, если число измерений равно четырем, следует считать, что индексы могут пробегать значения от 1 до 4, а не от 1 до 3, как предполагалось выше.
§ 3. Общее определение тензоров
Векторы, ковекторы, линейные операторы, и билинейные формы - примеры тензоров. Они являются геометрическими объектами, которые представляются в числовой форме, после того, как выбран базис в пространстве. Это числовое представление является своим для каждого из них: векторы и ковекторы представляются одномерными массивами, линейные операторы и квадратичные формы - двумерными массивами. Кроме количества индексов, имеет значение также и их расположение. Координаты вектора нумеруются одним верхним индексом, который называется контравариантным индексом. Координаты ковектора нумеруются одним нижним индексом, который называется ковариантным индексом. В матрице билинейной формы мы используем два нижних индекса; поэтому билинейные формы называют дважды-ковариантными тензорами. Линейные операторы - тензоры смешанного типа; их элементы нумеруются одним нижним и одним верхним индексами. Число индексов и их положения определяют правила преобразования, т.е. то как компоненты каждого конкретного тензора ведут себя при смене базиса. В общем случае, любой тензор представляет собой многомерный массив с определенным числом верхних и нижних индексов. Давайте обозначать число этих индексов через r и s. Тогда получится тензор типа (r,s); или иногда используется термин валентность. Тензор типа (r,s), или тензор валентности (r,s) - это r-раз контравариантный и s-раз ковариантный тензор.
Все это была терминология; теперь давайте перейдем к точному определению.
Оно базируется на следующих общих формулах преобразования:
$IMAGE64$ (3.1)
$IMAGE65$ (3.2)
Определение 1. Геометрический объект X, который в каждом базисе представляется (r + s)-мерным массивом $IMAGE66$вещественных чисел, удовлетворяющих правилам преобразования (3.1) и (3.2) при смене базиса, называется тензором типа (r,s), или валентности (r,s).
Индексы $IMAGE67$ и $IMAGE68$- свободные индексы. В правой стороне равенства (3.1) они распределены в S-ках и T-шках, каждый имеет только одно вхождение и сохраняет свою позицию при переходе из левой в правую часть равенства, т.е. верхние индексы $IMAGE67$ остаются верхними, а нижние индексы $IMAGE68$остаются нижними в правой части равенства (3.1).
Остальные индексы $IMAGE71$ и $IMAGE72$ - это индексы суммирования, они входят в правую часть (3.1) парами: один раз в качестве верхнего индекса и один раз в качестве нижнего индекса, один раз в S-матрице либо в T-матрице и второй раз среди индексов в компонентах массива $IMAGE73$.
При выражении $IMAGE66$ через $IMAGE73$ каждый верхний индекс обслуживается ровно один раз матрицей прямого перехода S, порождая при этом ровно одно суммирование в формуле (3.1):
$IMAGE76$ (3.3)
Подобным же образом, каждый нижний индекс обслуживается матрицей обратного перехода T и тоже порождает одно суммирование в формуле (1):
$IMAGE77$ (3.4)
Формулы (3.3) и (3.4) совпадают с (3.1), они записаны для того, чтобы сделать более понятным то, как записывается формула (3.1). Итак, определение тензоров дано.
§ 4. Скалярное произведение и метрический тензор
Ковекторы, линейные операторы и билинейные формы, те, что мы рассматривали выше, все это были искусственно построенные тензоры. Однако, есть некоторое количество тензоров естественного происхождения. Давайте вспомним, что мы живем в метрическом мире. Мы можем измерять расстояния между точками (следовательно, мы можем измерять длины векторов) и измерять углы между двумя направлениями в пространстве. Поэтому для любых двух векторов x и y мы можем определить их скалярное произведение:
(x,y) = |x||y| cos(φ), (4.1)
где φ - угол между векторами x и y. Это естественное скалярное произведение, порожденное нашей способнос