Курсовая работа

на тему: «Элементы общей топологии»

Введение

Топология – одна из самых молодых ветвей геометрии. Топология является одним из самых абстрактных разделов современной математики. Примерно за сто лет её существования в ней достигнуты результаты, важные для многих разделов математики.

Топология (от греческого «τοποξ» – место, окрестность, «λογοξ» – закон) – раздел математики, изучающий идеи непрерывности. В топологии впервые даются строгие определения таких фундаментальных понятий геометрии, как линия и поверхность. Предметом топологии являются свойства фигур, сохраняющиеся при гомеоморфизмах, то есть взаимно однозначных и непрерывных в обе стороны отображениях. Топология, как наука возникла из потребностей связанных с математическим анализом. Эта наука, хотя и считается молодой, на самом деле известна уже давно, именно благодаря тесным связям с математическим анализом. Идеи топологии идут от работ таких крупных математиков 19 в. как Риммман, Пуанкаре, Кантор, Эйлер. Развитие топологии идёт бурными темпами и в большом числе направлений, этот процесс не окончен в настоящее время, хотя ряд крупных проблем, стоящих перед топологией, успешно решен. Топологические методы стали мощным инструментом математического исследования. Топологический подход позволяет упростить многие доказательства фундаментальных теорем классической математики и обобщить эти теоремы на более широкие классы пространств.

Геометрия школьного курса имеет дело в основном со свойствами фигур, связанными с понятиями длины, площади, объема-то есть метрическими свойствами фигур. Лишь очень немногие теоремы и задачи школьного курса геометрии рассматривают свойства иного характера. Топология как раз и является разделом геометрии, изучающим свойства фигур, которые могут быть установлены без измерения и сравнения величин, но при этом имеющие геометрический смысл.

Целью первой главы курсовой работы было рассмотреть основные элементы общей топологии.

Задачи:

· дать определение топологического пространства;

· рассмотреть свойства топологических пространств;

· охарактеризовать топологические преобразования.

Во второй главе работы мы попытались рассмотреть топологические свойства поверхностей. Были поставлены следующие задачи:

· дать определение двумерного многообразия;

· рассмотреть эйлерову характеристику поверхности;

· охарактеризовать ориентируемые и неориентируемые поверхности.

1. Элементы общей топологии

1.1 Понятие топологического пространства

1.1.1 Понятие метрического пространства

Определение 1. Декартово произведение множеств А и В определяется как множество всех упорядоченных пар (х, у), где хÎА, уÎВ, то есть

А´В = {(х, у)| хÎА, уÎВ}.

В частности, возможно А = В.

Определение 2. Говорят, что в множестве Х задана метрика r, если определено отображение

r: Х ´ Х ® R,

удовлетворяющее следующим аксиомам:

1. " х, у Î Х { r (х, у) ³ 0}, причем r (х, у) = 0 Û х = у.

2. " х, у Î Х { r (х, у) = r (у, х)}.

3. " х, у, z Î Х {r (х, у) + r (у, z) ³ r (х, z)}.

Условия 1, 2, 3 называются аксиомами метрики, при этом условие 2 называется аксиомой симметрии, а 3 – аксиомой треугольника.

Определение 3. Множество Х с заданной на нем метрикой r называется метрическим пространством и обозначается (Х, r).

В тех случаях, когда ясно, о какой метрике идет речь, метрическое пространство (Х,r) обозначают просто Х.

Число r(х, у) называют расстоянием между точками х и у в пространстве Х.

1.1.2 Примеры метрических пространств

Пример 1. Определим для элементов произвольного непустого множества Х расстояние следующим образом:

r(х, у) = .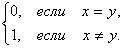

Очевидно, аксиомы 1 – 3 выполняются, а, следовательно, (Х, r) – метрическое пространство.

Пример 2. Множество действительных чисел R с расстоянием

r(х, у) = (у – х)² не является метрическим пространством.

Действительно не выполняется третья аксиома. Например, для трех точек 2, 3 и 4 получим:

r(2, 3) = (3 – 2)² = 1, r(3, 4) = (4 – 3)² = 1,

r(2, 4) = (4 – 2)² = 4 и r(2, 3) + r(3, 4) < r(2, 4).

Определение 1. Пусть (Х, r) – метрическое пространство, х₀ Î Х,

r > 0 – действительное число. Назовём открытым шаром с центром в точке х₀ и радиусом r множество

U (x₀, r) = {x | x Î X, r (x, x₀) < r }.

Определение 2. Подмножество G Ì Х будем называть открытым в

(Х, r), если любая его точка является центром некоторого открытого шара, содержащегося в G.

Пустое множество Æ также считаем открытым множеством.

Определение 3. Окрестностью точки А метрического пространства будем называть любое открытое множество, содержащее эту точку.

Обозначим совокупность всех открытых множеств в (Х, r) просто Ф_r.

Тогда имеет место следующая теорема.

Теорема. 1) Объединение любой совокупности {G_a} множеств из Ф_r принадлежит Ф_r.

G  Î Ф_r.

2) Пересечение любых двух множеств G₁ и G₂ из Ф_r принадлежит Ф_r.

G₁ ÇG₂ Î Ф_r.

3) Метрическое пространство Х – открытое множество, то есть

Х Î Ф_r, Æ Î Ф_r.

Доказательство. 1) Пусть 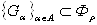. Обозначим

G = $IMAGE6$.

Возьмём произвольную точку х₀ Î G. Тогда существует такое a₀, что х₀ Î $IMAGE7$, и так как $IMAGE7$Î Ф_r, то найдётся число r₀, что

U (х₀, r₀) Ì $IMAGE6$.

Так как G ₀ Ì G, то U (х₀, r₀) Ì G.

Итак, G – открытое множество.

2) Пусть G = G₁ Ç G₂, где G₁, G₂ Î Ф_r и G $IMAGE11$ Æ.

Если х₀ Î G, то х₀ Î G₁ и х₀ Î G₂.

Тогда существуют такие радиусы r₁ и r₂, что

U(х₀, r₁) Ì G_1, U(х₀, r₂) Ì G₂.

Обозначим r = min {r₁, r₂}, тогда

U (х₀, r) Ì G₁ Ç G₂ = G.

Итак, G – открытое множество.

3. Так как всегда можно представить

Х = $IMAGE12$,

где U_a – открытый шар радиуса r, с центром в точке , объединение рассматривается по всем точкам пространства, то в силу 1 получим, что пространство Х – открыто. Пустое множество мы предполагаем всегда открытым.

В дальнейшем описанное нами семейство Ф_r всех открытых множеств в метрическом пространстве (Х, r) будем называть топологией, индуцированной метрикой r в Х._.

1.1.3 Определение и примеры топологических пространств

Многие понятия теории метрических пространств (предел, предельная точка, точка прикосновения, замыкание множества, граница множества, непрерывность и т.д.) вводятся, опираясь на понятие окрестности или, что тоже самое, на понятие открытого множества. Понятие окрестность и открытое множество определяются с помощью метрики.

Свойства открытых множеств метрического пространства принимаются в качестве аксиом. Этот путь приводит нас к топологическим пространствам, по отношению к которым метрические пространства представляют собой частный случай.

Определение 1. Пусть Х – непустое множество элементов произвольной природы, Ф = { $IMAGE6$} – семейство подмножеств множества Х, удовлетворяющее следующим аксиомам:

1. Само множество Х и пустое множество Æ принадлежат семейству Ф.

2. Объединение любого семейства множеств из Ф также принадлежит Ф.

3. Пересечение любых двух множеств из Ф также принадлежит Ф.

Тогда семейство Ф называется топологией или топологической структурой.

Пара (Х, Ф) или, другим словами, множество Х, в котором задана некоторая топология, называется топологическим пространством.

Элементы множества Х называются точками топологического пространства, элементы семейства Ф называются открытыми множествами в (Х, Ф).

Когда не может возникнуть недоразумений, разрешается просто писать: Х – топологическое пространство, G  – открытое множество, то есть не указывать постоянно связь с топологией Ф.

Примеры топологических пространств.

Пример 1. Х – произвольное множество. Из аксиомы 1 топологического пространства вытекает, что среди открытых множеств любой топологической структуры в Х обязательно должны быть пустое множество Æ и само множество Х. Очевидно, что для семейства

Ф_т = {Æ, X},

которое состоит лишь из этих двух множеств, выполняются также и аксиомы 2 и 3.

Поэтому Ф_т = {Æ, X} является простейшей топологической структурой в Х. Эта топология называется тривиальной, а пара (Х, Ф) тривиальным топологическим пространством. Иногда эту пару называют антидискретным топологическим пространством.

Пример 2. Другой крайностью является так называемое дискретное топологическое пространство (Х, Ф_d), где Ф_d представляет собой семейство всех подмножеств множества Х. Очевидно, что и в этом случае все аксиомы 1 – 3 выполняются.

Пример 3. Пусть Х = R³. Открытыми в Х множествами назовем только открытые шары U(r) с общим центром О и радиусом r, а также всё множество Х и пустое множество.

Очевидно, аксиома 1 выполняется.

Пусть {U(r_a)} – любая система открытых множеств. Тогда их объединением будет шар с центром О и радиусом r = $IMAGE16$.

Если $IMAGE16$ = ¥, то U(r) = X.

Следовательно, аксиома 2 выполняется.

Пересечением двух множеств U(r₁) и U(r₂) будет множество U(r), где r = $IMAGE18$, то есть аксиома 3 также выполняется.

Выделенное нами семейство открытых множеств является топологией в R³, которую иногда называют концентрической.

Определение 2. Пусть в множестве Х введены две топологии Ф₁ и Ф₂. Говорят, что Ф₁ сильнее Ф₂ (или Ф₂ слабее Ф₁₎, если Ф₂ Ì Ф₁, то есть любое множество из Ф₂ принадлежит Ф₁.

Очевидно, самой сильной топологией является дискретная топология, а самой слабой – тривиальная.

А вообще – две топологии на одном и том же множестве могут быть несравнимыми.

Пример.

Х = $IMAGE19$,

Ф₁ = {Æ, Х, $IMAGE20$},

Ф₂ = {Æ, Х, $IMAGE21$}.

Топологии Ф₁ и Ф₂ несравнимы.

Теорема 1. Пересечение произвольного множества топологий, заданных на Х, является топологией в Х. Эта топология Ф слабее любой из данных топологий Ф .

Доказательство. Пусть $IMAGE23$.

Так как для любого a

{Х, Æ} Ì Ф ,

то

{X, Æ} Ì Ф.

Далее, из того, что каждое Ф  замкнуто относительно взятия любых объединений и конечных пересечений, следует, что этим свойством обладает и множество $IMAGE23$.

Теорема 2. Пусть А – произвольная система подмножеств множества Х. Тогда существует минимальная топология в Х, содержащая А.

Действительно, всегда существуют топологии, содержащие А, например, дискретная. Пересечение всех топологий, содержащих А и есть искомая топология. Эта минимальная топология называется топологией, порождённой системой А.

1.2 Свойства топологических пространств

1.2.1 Понятие подпространства

Если У подмножество Х, а (Х, Ф) – топологическое пространство, то на У можно рассматривать топологию

y = { $IMAGE6$Ç У | G  Î Ф }.

Действительно, обозначим:

S  = $IMAGE6$Ç У, y = { S }.

1. $IMAGE32$ Þ Æ, У Î Y.

2.  S  = (G $IMAGE36$Ç У) = ( G )Ç У Î y.

3. S  Ç S $IMAGE40$ = (G Ç У) Ç (G $IMAGE40$Ç У) = (G ÇG $IMAGE40$) Ç У Î y.

(У, y) – называют топологическим подпространством пространства (Х, Ф), а y – топологией, индуцированной топологией Ф.

Пример. Пусть Х = Е³. Открытыми в Х множествами назовем только открытые шары U(r) с общим центром О и радиусами r, а также все множество Х и пустое множество. Известно, что набор