Содержание

Введение

Глава 1. Неравенство Маркова на индексационных классах

§ 1. Экстремальная задача

§ 2. Свойства отображения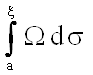

§ 3. Доказательство теоремы

Глава 2. О чебышевской экстремальной задаче на [0, ¥)

Литература

Введение

В работе вводится понятие индекса функции на [0,¥) относительно произвольного класса F функций на [0, ¥), основанное на сравнении двух функций через количество перемен знака их разности. С помощью понятия индекса аксиоматически определяется индексационный класс F. На индексационных классах изучается конечная проблема моментов.

Определение 1. Скажем, что функция D(t), tÎR¹, имеет k строгих перемен знака, если существуют множества A₁<A₂<…<A_k+1, такие, что

а) ;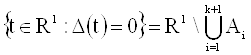

б) знаки функции D(t) на множествах A₁, A₂, …, A_k+1 перемежаются.

Пусть f(t) и g(t) – функции на R¹. Пишем 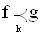, если функция D=g-f имеет k-1 строгих перемен знака, причем на последнем множестве строгого знакопостоянства она отрицательна.

Нетрудно видеть, что отношение 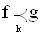 выполнено тогда и только тогда, когда

а) не существует точки x₁, …, x_k (-¥<x₁<…<x_k<¥) такие, что

(-1)^k-i f(x_i) > (-1)^k-i g(x_i), ;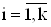

б) существуют точки y₁, …, y_k (-¥<y₁<…<y_k<¥) такие, что

(-1)^k-i f(y_i) > (-1)^k-i g(y_i), .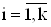

Пусть F – некоторый класс непрерывных слева функций на [0, ¥) и f, g Î F.

Определение 2. Пишем $IMAGE7$, если для любой функции hÎF, h¹g, выполнено одно из отношений: $IMAGE8$, $IMAGE9$ , $IMAGE10$, $IMAGE11$. Пишем $IMAGE12$, если для любой функции hÎF, h¹f, выполнено одно из отношений: $IMAGE13$, $IMAGE9$ , $IMAGE15$, $IMAGE11$.

Функция f имеет индекс k^- в F, если выполнено отношение $IMAGE12$ и не выполнено $IMAGE18$. Функция g имеет индекс k⁺ в F, если выполнено $IMAGE7$ и не выполнено $IMAGE20$.

Через I_k^- (I_k⁺), k³1, обозначим совокупность всех функций с индексом k^- (k⁺) в F.

Пусть U – семейство функций на [0, ¥).

Через F_U обозначим множество функций fÎF, для которых интегралы

$IMAGE21$, uÎU,

абсолютно сходятся.

В случае $IMAGE22$ положим $IMAGE23$, fÎF_U, AÌF_U, $IMAGE24$:

_$IMAGE25$, F_i(A)={F_i(f): fÎA},

$IMAGE26$, $IMAGE27$,

$IMAGE28$.

Множество $IMAGE29$ называется моментным пространством класса F относительно системы функций $IMAGE30$.

Лемма 1. Пусть системы u₁(t), …, u_n(t) и u₁(t), …, u_n(t), u_n+1(t) образуют T₊-системы на [0, ¥) такие, что $IMAGE31$. Тогда отношение $IMAGE32$ невозможно для $IMAGE33$ и, если $IMAGE34$, то

$IMAGE35$.

Доказательство. Допустим, что 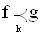, где k£n, и A₁, …, A_k – множества строгого знакопостоянства функции D=g - f. Для векторов $IMAGE37$ рассмотрим матрицу

$IMAGE38$.

Так как

$IMAGE39$, $IMAGE40$,

то есть

$IMAGE41$, (1)

где d_i(-1)^k-i, 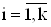 и d_i=0, $IMAGE43$ для всех векторов $IMAGE44$.

Из (1) следует, что detH( $IMAGE44$)=0 для любых $IMAGE44$. С другой стороны, применив k раз теорему о среднем к H( $IMAGE44$), получим

$IMAGE48$, (2)

где 0£x₁<x₂<…<x_k<¥. Так как векторы $IMAGE49$ линейно зависимы, то их можно дополнить до системы линейно независимых векторов $IMAGE50$  $IMAGE51$. Из (2) получаем $IMAGE52$.

Пусть теперь $IMAGE34$ и $IMAGE54$.

Так как

$IMAGE55$, (3)

где d_i=(-1)^n+1-i, $IMAGE56$, то

$IMAGE57$,

где H – матрица, записанная в (3) слева, $IMAGE58$- матрица, получаемая из H удалением (n+1)-ых строки и столбца. Применив теорему о среднем, получаем detH>0, $IMAGE59$. Вместе с равенством d_n+1=1 это означает, что d>0.

Определение 3. Скажем, что последовательность {f_i}_i³1 функций на [0, ¥) относительно класса U слабо сходится к функции f $IMAGE60$, если

$IMAGE61$

для всех uÎU.

Определение 4. Множество AÌF_U назовем (k, U) окрестностью функции f в F, если fÎA и множество А имеет вид $IMAGE62$, где V открыто, $IMAGE63$ при $IMAGE64$, $IMAGE65$ при $IMAGE66$  $IMAGE67$.

Множество AÌF_U назовем (k, U)-открытым, если каждая функция fÎA имеет (k, U) окрестность, состоящую из функций множества А.

Определение 5. Класс F непрерывных слева, неотрицательных функций на [0, ¥) назовем нижним U-индексационным с дефектом n, если:

1. Класс F равномерно ограничен, то есть существует L>0, такое, что f(t)£L при t³0, fÎF;

2. $IMAGE68$;

3. Множества I_k^- (k-1, U) – открыты для всех k>n+1;

4. Из любой последовательности {f_i}_i³1ÌI^-_k+1 (k>n) такой, что

$IMAGE69$,

можно выделить подпоследовательность, слабо относительно класса U сходящуюся к некоторой функции $IMAGE70$.

Пусть система $IMAGE71$ образует T₊ - систему на [0, ¥).

Рассмотрим систему функций $IMAGE72$, такую, что w_i=u_i для $IMAGE73$ и $IMAGE74$ - T₊ - системы для m³n (см. [1]).

Теорема 1. Пусть система $IMAGE75$ образует T₊ - систему на [0, ¥), F-нижний W-индексационный с дефектом n класс функций на [0, ¥). Тогда

$IMAGE76$.

Доказательство. Пусть $IMAGE77$. Согласно условию 2 определения индексационного класса, существует последовательность {f_j}_j³1ÌI_k^- такая, что $IMAGE78$. Зафиксируем произвольное f_l.

Если f_lÎI_k^-, где k£n+1, то положим f_l^*=f_l.

Пусть k>n+1 и s={ $IMAGE79$} – (k-1, W) окрестность f_l в I_k^-.

Рассмотрим произвольные $IMAGE80$ и $IMAGE81$ $IMAGE82$. Допустим, что $IMAGE83$. Согласно лемме 1, отношения $IMAGE84$и $IMAGE85$ невозможны для s£k-1. Следовательно, $IMAGE86$ и $IMAGE87$, что невозможно.

Таким образом, отображение $IMAGE88$ непрерывно и взаимно однозначно. Из принципа инвариативности области (см. [3]) следует, что $IMAGE89$ - открытое множество в R^k-1, содержащее $IMAGE90$.

Пусть $IMAGE91$, $IMAGE92$ и $IMAGE93$ - многочлен по системе $IMAGE94$, имеющий k-2 нулей x₁, …, x_k-2. Условие b_k-1=0 противоречит чебышевости системы $IMAGE95$. Положим b_k-1>0. Тогда (см. [5]) P(t)>0 при t>x_k-2.

Имеем

$IMAGE96$,

где c_lⁱ – i-ая компонента вектора $IMAGE97$, и, следовательно,

$IMAGE98$.

Так как константа К не зависит от f, то m_l >-¥.

Кроме того, $IMAGE99$.

Возьмем последовательность $IMAGE100$, такую, что

F_k-1(f_lp)>F_k-1(f_lq)=m_l при p<q и

$IMAGE101$,

Рассмотрим произвольные f_lp и f_lq, где p<q. Так как $IMAGE102$, то отношения $IMAGE103$ и $IMAGE104$ невозможны для s£k-2. Отношения $IMAGE105$ и $IMAGE106$ невозможны, так как f_lp, f_lqÎI_k^-. Из леммы 1 получаем $IMAGE107$.

Так как $IMAGE108$, то найдется функция $IMAGE109$, такая, что F_k-1(f_l^’)=m_l.

Отношение f_l^’ÎI_k^- невозможно, в силу определения числа m_l и принципа инвариативности области. Отношения f_l^’ÎI_m^- для m<k-1 невозможны, так как $IMAGE110$. Следовательно $IMAGE111$.

Продолжая таким образом, через k-n-2 шагов получим функцию $IMAGE112$, такую, что $IMAGE113$. Из условия $IMAGE114$ следует утверждение теоремы 1.

Замечание 1. Класс F непрерывных слева, неотрицательных функций на [0, ¥) назовем верхним U-индексационным с дефектом n, если:

1. Класс F равномерно ограничен;

2. $IMAGE115$;

3. Множества I_k⁺ (k-1, U) – открыты для всех k>n+1;

4. Для k>n из любой последовательности {f_i}_i³1ÌI_k⁺ такой, что

$IMAGE69$,

можно выделить подпоследовательность, относительно класса U слабо сходящуюся к некоторой функции $IMAGE117$;

5. I_k⁺ÌF_U для k³n+1.

Теорема 2. Пусть система $IMAGE118$ образует T₊-систему на [0, ¥), F-верхний W-индексационный с дефектом n класс функций на [0, ¥). Тогда

$IMAGE119$.

Определение 6. Систему $IMAGE120$ непрерывных на [0, ¥) функций назовем T₊¹-системой, если она является T₊-системой, и, кроме того, системы u₁, …, u_l-1, u_l+1, …, u_n также являются T₊-системами для $IMAGE121$.

Лемма 2. Пусть $IMAGE122$- T₊¹-система на [0, ¥), функции f и g таковы, что

(-1)^n-i F_i(f) ³ (-1)^n-i F_i(g), $IMAGE73$.

Тогда отношения $IMAGE124$, $IMAGE33$ и $IMAGE126$, $IMAGE127$, невозможны.

Доказательство. Допустим, что имеет место отношение $IMAGE128$ и 1£p£n.

Пусть x₁, …, x_p-1 (-¥<x₁<…<x_p-1<¥) – точки перемен знака функции $IMAGE129$; x_о=-¥, x_n=¥; $IMAGE130$. Выберем точки x_n-1<x_n-2<…<x_p<x_p-1 так, чтобы $IMAGE131$, $IMAGE132$, $IMAGE133$. Рассмотрим систему равенств

$IMAGE134$, (4)

где h_i=±1. Из условия $IMAGE128$ следует, что h_n=1. С другой стороны, из (4) получаем

$IMAGE136$,

где А – матрица, записанная в (4) слева, A_nⁱ – матрица, получаемая из А удалением i-ой строки и n-го столбца. Так как $IMAGE120$- T₊¹-система на [0, ¥), то detA>0, detA_nⁱ>0, $IMAGE73$. Следовательно, h_n£0. Получили противоречие.

Случай $IMAGE139$, $IMAGE140$, рассматривается аналогично.

Теорема 3. Пусть $IMAGE71$- T₊¹-система на [0, ¥), F-нижний W-индексационный с дефектом n класс функций на [0, ¥). Тогда

$IMAGE142$.

Доказательство. Пусть $IMAGE143$. Возьмем последовательность векторов $IMAGE144$ так, чтобы $IMAGE145$ при $IMAGE146$ и

$IMAGE147$

для $IMAGE73$, j³1.

Согласно теореме 1, для любого $IMAGE149$ найдется последовательность $IMAGE150$ такая, что $IMAGE151$.

Существует j₁, такое, что $IMAGE152$, где r - какая-либо метрика в Rⁿ, и

$IMAGE153$, $IMAGE154$.

Выберем j₂ так, чтобы $IMAGE155$ и

$IMAGE156$, $IMAGE73$.

Продолжая таким образом, получим последовательность $IMAGE158$ такую, что $IMAGE159$ и

$IMAGE160$ (5)

Рассмотрим произвольные $IMAGE161$ и $IMAGE162$. Отношения $IMAGE163$ и $IMAGE164$для k>n невозможны, в силу условий $IMAGE165$.

Из неравенств (5), в силу леммы 2, имеем

$IMAGE166$,

т. е. существует функция $IMAGE167$ такая, что $IMAGE168$. Включение $IMAGE169$ противоречит условию $IMAGE143$, в силу принципа инвариативности области.

Из произвольности $IMAGE143$ следует утверждение теоремы 2.

Глава 1 Неравенство Маркова на индексационных классах

§ 1 Экстремальная задача

Пусть Â – некоторый класс функций распределения (ФР) на [a, b], -¥<a<b<¥; W(t) – (n+1) раз непрерывно дифференцируемая функция на [a, b], причем W^(k)(t)>0 для tÎ[a, b] и $IMAGE172$; c₁, …, c_n – вещественные константы; xÎ[a, b].

Экстремальная задача. Найти супремум и инфимум интеграла

$IMAGE173$

на множестве $IMAGE174$  $IMAGE175$ ФР из Â, удовлетворяющих ограничениям

$IMAGE176$, $IMAGE177$.

Для классов Â_o - всех ФР на [a, b] и В_L