Курсовая работа
Выполнил студент 2го курса ФМФ группы «Б» Симонян Сергей Олегович
Ставропольский Государственный университет
Кафедра математического анализа
Ставрополь, 2004 г.
Введение.
Функция – одно из основных понятий во всех естественнонаучных дисциплинах. Не случайно ещё в средней школе дети получают интуитивное представление об этом понятии. Со школьной скамьи наш багаж знаний пополняется сведениями о таких функциях как линейная, квадратичная, степенная, показательная, тригонометрические и других. В курсе высшей математики круг известных функций значительно расширяется. Сюда добавляются интегральные и гиперболические функции, эйлеровы интегралы (гамма- и бета-функции), тета-функции, функции Якоби и многие другие.
Что же такое функция? Строгого определения для неё не существует. Это понятие является в математике первичным, аксиоматизируется. Однако, под функцией понимают закон, правило, по которому каждому элементу какого-то множества X ставится в соответствие один или несколько элементов множества Y. Элементы множества X называются аргументами, а множества Y – значениями функции. Если каждому аргументу соответствует одно значение, функция называется однозначной, если более одного – то многозначной. Синонимом функции является термин «отображение». В простейшем случае множество X может быть подмножеством поля действительных R или комплексных C чисел. Тогда функция называется числовой. Нам будут встречаться только такие отображения.
Функции могут быть заданы многими различными способами: словесным, графическим, с помощью формулы. Функция, которую мы будем рассматривать в этой работе, задаётся через бесконечный ряд. Но, несмотря на такое нестандартное определение, по своему представлению в виде ряда она может быть хорошо изучена методами теории рядов и плодотворно применена к различным теоретическим и прикладным вопросам математики и смежных с ней наук.
Конечно же, речь идёт о знаменитой дзета-функции Римана, имеющей широчайшие применения в теории чисел. Впервые ввёл её в науку великий швейцарский математик и механик Леонард Эйлер и получил многие её свойства. Далее активно занимался изучением дзета-функции немецкий математик Бернгард Риман. В честь него она получила своё название, так как он опубликовал несколько исключительно выдающихся работ, посвящённых этой функции. В них он распространил дзета-функцию на область комплексных чисел, нашёл её аналитическое продолжение, исследовал количество простых чисел, меньших заданного числа, дал точную формулу для нахождения этого числа с участием функции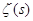 
и высказал свою гипотезу о нулях дзета-функции, над доказательством или опровержением которой безрезультатно бьются лучшие умы человечества уже почти 150 лет.
Научная общественность считала и считает решение этой проблемы одной из приоритетных задач. Так Давид Гильберт, выступавший на Международной Парижской математической конференции 1900 году с подведением итогов развития науки и рассмотрением планов на будущее, включил гипотезу Римана в список 23 проблем, подлежащих решению в новом столетии и способных продвинуть науку далеко вперёд. А на рубеже веков, в 2000 году американский The Clay Mathematics Institute назвал семь задач, за решение каждой из которых будет выплачен 1 миллион долларов. В их число также попала гипотеза Римана.
Таким образом, даже бы поверхностное знакомство с дзета-функцией будет и интересным, и полезным.
Глава 1.
Итак, приступим к изучению этой важной и интересной дзета-функции Римана. В данной главе мы получим некоторые свойства функции в вещественной области, исходя из её определения с помощью ряда.
Определение. Дзета-функцией Римана ζ(s) называют функцию, которая любому действительному числу s ставит в соответствие сумму ряда
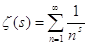(1)
если она существует.
Основной характеристикой любой функции является область определения. Найдём её для нашей функции.
Пусть сначала s≤0, тогда s=−t, где t принадлежит множеству неотрицательных действительных чисел R+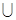 
{0}. В этом случае 
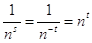и ряд (1) обращается в ряд 
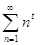, который, очевидно, расходится как при t>0, так и при t=0. То есть значения s≤0 не входят в область определения функции.
Теперь пусть s>0. Для исследования сходимости ряда (1) воспользуемся интегральным признаком Коши. При каждом s рассмотрим функцию $IMAGE6$, где $IMAGE7$, которая является на промежутке непрерывной, положительной и монотонно убывающей. Возникает три различных возможности:
0<s<1. Тогда $IMAGE8$, поэтому ряд (1) расходится и промежуток (0;1) не входит в область определения дзета-функции;
s=1. Получаем $IMAGE9$, то есть при s=1 дзета-функция Римана также не определена;
s>1. В этом случае $IMAGE10$
$IMAGE11$. Ряд (1) сходится.
Обобщив результаты, находим, что область определения дзета-функции есть промежуток $IMAGE12$. На этом промежутке функция оказывается непрерывной и дифференцируемой бесконечное число раз.
Докажем непрерывность функции ζ(s) на области определения. Возьмём произвольное число s0>1. Перепишем ряд (1) в виде $IMAGE13$. Как было выше показано, ряд $IMAGE14$ сходится, а функции $IMAGE15$ при s>s0 монотонно убывают и все вместе ограничены единицей. Значит, по признаку Абеля для s>s0 ряд (1) сходится равномерно. Используя теорему о непрерывности суммы функционального ряда, получаем, что в любой точке s>s0 дзета-функция непрерывна. Ввиду произвольности s0 ζ(s) непрерывна на всей области определения.
Теперь почленным дифференцированием ряда (1), пока формально, найдём производную дзета-функции Римана:
$IMAGE16$ (2).
Чтобы оправдать этот результат, достаточно удостовериться в том, что ряд (2) равномерно сходится на промежутке $IMAGE17$ и воспользоваться теоремой о дифференцировании рядов. Используем тот же приём. Зафиксируем любое s0>1 и представим ряд (2) в виде $IMAGE18$ для s>s0. Множители $IMAGE19$, начиная с n=2, монотонно убывают, оставаясь ограниченными числом ln 2. Поэтому по признаку Абеля ряд (2) сходится равномерно при s>s0, а значит и при любом s>1. Какое бы значение s>1 ни взять его можно заключить между $IMAGE20$ и $IMAGE21$, где $IMAGE22$, а $IMAGE23$; к промежутку $IMAGE24$ применима вышеуказанная теорема.
Таким же путём можно убедиться в существовании для дзета-функции производных всех порядков и получить их выражения в виде рядов:
$IMAGE25$.
Попытаемся построить наглядное изображение функции в виде графика. Для этого изучим сначала её поведение на бесконечности и в окрестности точки s=1.
В первом случае, ввиду равномерной сходимости ряда (1), по теореме о почленном переходе к пределу, имеем $IMAGE26$. При n=1 предел равен единице, остальные пределы равны нулю. Поэтому $IMAGE27$.
Чтобы исследовать случай $IMAGE28$, докажем некоторые вспомогательные оценки.
Во-первых, известно, что если для ряда $IMAGE29$ существует непрерывная, положительная, монотонно убывающая функция $IMAGE30$, определённая на множестве $IMAGE31$, такая, что $IMAGE32$, и имеет первообразную $IMAGE33$, то остаток ряда оценивается так: $IMAGE34$, где $IMAGE35$. Применяя вышесказанное к ряду (1), найдём, что необходимая функция
$IMAGE6$, а $IMAGE37$ и $IMAGE38$. Отсюда, подставляя в двойное неравенство, имеем
$IMAGE39$ (3). В левом неравенстве положим n=0, тогда $IMAGE40$, то есть $IMAGE41$. В правом же возьмём n=1 и получим $IMAGE42$, далее $IMAGE43$, $IMAGE44$ и, наконец, $IMAGE45$. Переходя в неравенствах $IMAGE46$ к пределу при $IMAGE28$, находим $IMAGE48$.
Отсюда, в частности, следует, что $IMAGE49$. Действительно, положим $IMAGE50$. Тогда $IMAGE51$, то есть $IMAGE52$ $IMAGE53$. Поэтому $IMAGE54$. Из того, что $IMAGE55$, а $IMAGE56$, вытекает доказываемое утверждение.
Можно, однако, получить ещё более точный результат для оценки поведения дзета-функции в окрестности единицы, чем приведённые выше, принадлежащий Дирихле. Будем отталкиваться от очевидного при произвольном n равенства $IMAGE57$. Прибавим ко всем частям неравенств (3) сумму $IMAGE58$ и вычтем $IMAGE59$. Имеем $IMAGE60$. Пусть здесь s стремится к единице. По правилу Лопиталя легко вычислить $IMAGE61$ и $IMAGE62$. Мы пока не знаем, существует ли предел выражения $IMAGE63$ при $IMAGE28$, поэтому, воспользовавшись наибольшим и наименьшим пределами, напишем неравенства так: $IMAGE65$
$IMAGE66$. Ввиду произвольности n возьмём $IMAGE67$. Первое и последнее выражения стремятся к эйлеровой постоянной C (C $IMAGE68$0,577). Значит $IMAGE69$, а, следовательно, существует и обычный предел и $IMAGE70$.
Найденные выше пределы позволяют получить лишь приблизительное представление о виде графика дзета-функции. Сейчас мы выведем формулу, которая даст возможность нанести на координатную плоскость конкретные точки, а именно, определим значения $IMAGE71$, где k – натуральное число.
Возьмём известное разложение $IMAGE72$, где $IMAGE73$ - знаменитые числа Бернулли (по сути, через него эти числа и определяются). Перенесём слагаемое $IMAGE74$ в левую часть равенства. Слева получаем $IMAGE75$ $IMAGE76$cth $IMAGE74$, а в правой части - $IMAGE78$, то есть $IMAGE74$cth $IMAGE80$. Заменяем $IMAGE81$ на $IMAGE82$, получаем $IMAGE83$cth $IMAGE84$.
С другой стороны, существует равенство cth $IMAGE85$, из которого $IMAGE81$cth $IMAGE87$. Подстановкой $IMAGE83$ вместо $IMAGE81$ находим $IMAGE83$cth $IMAGE91$ $IMAGE92$. Если $IMAGE93$, то для любого $IMAGE94$N $IMAGE95$ $IMAGE96$ и по теореме о сложении бесконечного множества степенных рядов $IMAGE83$cth $IMAGE98$ $IMAGE99$.
Приравняем полученные разложения: $IMAGE100$
$IMAGE101$, следовательно $IMAGE102$. Отсюда немедленно следует искомая формула
$IMAGE103$ (4), где $IMAGE104$ - k-е число Бернулли. Она удобна тем, что эти числа хорошо изучены и для них составлены обширные таблицы.
Теперь, исходя из полученных результатов, можно построить эскиз графика дзета-функции Римана, достаточно хорошо отражающий её поведение на всей области определения.
$IMAGE105$
Леонард Эйлер, впервые рассмотревший дзета-функцию, получил замечательное разложение её в бесконечное произведение, которое иногда тоже принимают за определение:
$IMAGE106$, где pi – i-е простое число (4).
Докажем тождественность ряда (1) и произведения (4). Вспомнив формулу суммы геометрической прогрессии, получаем равенство $IMAGE107$
$IMAGE108$ Если перемножить конечное число таких рядов, отвечающих всем простым числам, не превосходящим заданного натурального числа N, то получившееся частичное произведение окажется равным $IMAGE109$, где символ * означает, что суммирование распространяется не на все натуральные числа, а лишь на те из них (не считая единицы), которые в своём разложении содержат только простые числа меньшие N. Так как первые N натуральных чисел этим свойством обладают, то
$IMAGE110$ (5).
Сумма $IMAGE111$ содержит не все числа, большие N+1, поэтому, очевидно, $IMAGE112$. Из (5) получаем
$IMAGE113$ (6).
Ввиду сходимости ряда (1), выражение справа, представляющее его остаток после N-го члена, стремится к нулю при N стремящимся к бесконечности, а $IMAGE114$ есть произведение (4). Значит из неравенства при $IMAGE115$ $IMAGE116$, что и требовалось доказать.
Формула (4) важна потому, что она связывает натуральный ряд, представленный множеством значений аргумента дзета-функции, со множеством простых чисел. Ещё один шаг в этом направлении мы сделаем, оценив $IMAGE117$, а именно показав, что $IMAGE118$, где $IMAGE119$ остаётся ограниченным при $IMAGE28$.
Из (4) следует, что $IMAGE121$, где $IMAGE122$N, а $IMAGE123$ при $IMAGE115$. Возьмём логарифм от обеих частей равенства, тогда $IMAGE125$ $IMAGE126$. Натуральные логарифмы под знаком суммы разлагаются в ряд: $IMAGE127$ $IMAGE128$. Подставив полученные разложения в равенство и устремив N к бесконечности, имеем $IMAGE129$. Остаётся доказать ограниченность последнего слагаемого. Ясно, что $IMAGE130$. Последнее равенство справедливо, так как $IMAGE131$ $IMAGE132$. Далее, очевидно, $IMAGE133$, что и завершает доказательство.
На этом закончим изложение свойств дзета-функции Римана для действительного аргумента, так как наибольший теоретический и прикладной интерес представляет случай изложенный во второй главе.
Глава 2.
Все результаты первой главы, касающиеся дзета-функции Римана, были получены в предположении, что её аргумент s – действительное число. Однако, самые выдающиеся исследования и многочисленные важные приложения стали возможны лишь после включения в область определения функции комплексных чисел. Впервые рассмотрел дзета-функцию как функцию мнимого аргумента немецкий математик Бернгард Риман, глубоко изучивший её свойства и широко применявший её в теории чисел. В честь него функция получила своё название.
Для комплексной дзета-функции остаётся в силе определение, данное в главе 1, с тем лишь изменением, что теперь там будет $IMAGE