Министерство образования Российской Федерации
Институт дистанционного образования
ГОУ ВПО « Тюменский государственный университет »
Контрольная работа
по дисциплине: «Высшая математика»
Тема: «ДВОИНЫЕ ИНТЕГРАЛЫ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА»
УК (220501.65)/3. сокращенная
Выполнил студент Петренко Н. В.
Нижневартовск 2010
Контрольная работа
Вариант 5
1. Вычислить интегралы:
1.1. 
где D – прямоугольник 
1.2.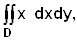 
где D – область, ограниченная линиями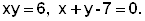 
2. Найти общее решение уравнений:
2.1. 
2.2. $IMAGE6$
Решение контрольной работы.
1. где D – прямоугольник
Построим область D:
$IMAGE9$
Сводя двойной интеграл к повторному и расставляя пределы, получаем:
$IMAGE10$
Ответ: I=20.
2. 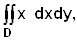где D – область, ограниченная линиями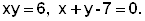
Построим область D, которая ограничена ветвью гиперболы у=6/х, расположенной в первой четверти и прямой у=7-х. Находим точки пересечения: 6/х=7-х; $IMAGE13$, откуда х=1 и х=6. Имеем две точки (1;6) и (6;1).
$IMAGE14$
Запишем границы области D: $IMAGE15$ Сводя двойной интеграл к повторному и расставляя пределы, получаем:
$IMAGE16$
=126-72-36-7/2+1/3+6=24-19/6=(144-19)/6=125/6.
Ответ: I=125/6.
3.
Характеристическое уравнение $IMAGE18$имеет кратные корни k=2, поэтому общее решение имеет вид: $IMAGE19$.
Ответ: $IMAGE19$.
4. $IMAGE6$
Это линейное неоднородное дифференциальное уравнение (ЛНДУ). Решением ЛНДУ является сумма решений соответствующего однородного (ЛОДУ) и любого частного решения. Решаем ДУ: у''+y'-2=0. Характеристическое уравнение $IMAGE22$ имеет корни k =-2 и k=1, поэтому общее решение однородного ДУ имеет вид: $IMAGE23$. Частное решение будем искать в виде: $IMAGE24$. Дважды дифференцируем последнее: $IMAGE25$. Подставляем в заданное ДУ и приравниваем коэффициенты:
$IMAGE26$, откуда В=-3, С=-3, D=-4,5. Запишем общее решение заданного неоднородного ДУ: $IMAGE27$.
Ответ: $IMAGE27$.