Министерство образования Республики Беларусь

Гомельский Государственный университет имени Франциска Скорины

Курсовая работа

«Дифференциальные системы, эквивалентные автономным системам с известным первым интегралом»

Гомель 2006

Реферат

Курсовая работа состоит из 19 страниц, 3-х источников.

Ключевые слова: эквивалентная система, первый интеграл дифференциальной системы, отражающая функция, эквивалентность систем в смысле совпадения отражающих функций, непрерывно дифференцируемая функция, непрерывная скалярная нечётная функция.

Целью курсовой работы является нахождение связи между первым интегралом системы и эквивалентными системами.

Содержание

Введение

Отражающая функция

Первый интеграл дифференциальной системы и условия его существования

Возмущения дифференциальных систем, не изменяющих временных симметрий

Общее решение

Заключение

Список использованных источников

Введение

В курсовой работе мы находим связь между первым интегралом и эквивалентными системами.

В результате приходим к теореме, которая звучит так:

Пусть 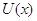 первый интеграл системы 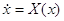,  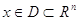(1). Если 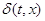, удовлетворяет уравнению 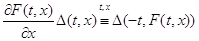, то указанная система эквивалентна системе $IMAGE6$, $IMAGE7$,  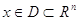(2). И если, кроме того $IMAGE9$, где $IMAGE10$- некоторая функция ( $IMAGE10$-может равняться const), тогда первый интеграл системы (2) выражается следующей формулой $IMAGE12$, где $IMAGE13$ и $IMAGE14$.

Отражающая функция

Определение. Рассмотрим систему

$IMAGE15$ (1)

cчитая, что правая часть которой непрерывна и имеет непрерывные частные производные по $IMAGE16$. Общее решение в форме Коши обозначено через $IMAGE17$). Через $IMAGE18$обозначим интервал существования решения $IMAGE19$.

Пусть

$IMAGE20$

Отражающей функцией системы (1) назовём дифференцируемую функцию $IMAGE21$, определяемую формулой

$IMAGE22$

Для отражающей функции справедливы свойства:

1.) для любого решения $IMAGE23$системы (1) верно тождество

$IMAGE24$

2.) для отражающей функции F любой системы выполнены тождества

$IMAGE25$

3) дифференцируемая функция $IMAGE21$ будет отражающей функцией системы (1) тогда и только тогда, когда она удовлетворяет системе уравнений в частных производных

$IMAGE27$

и начальному условию

$IMAGE28$

Рассмотрим систему $IMAGE29$ (1*) считая, что её правая часть непрерывно дифференцируемая. Будем говорить, что множество систем вида (1*) образует класс эквивалентности, если существует дифференцируемая функция $IMAGE21$ со свойствами: 1) отражающая функция $IMAGE31$ любой системы из рассматриваемого множества совпадает в области определения $IMAGE32$ с функцией $IMAGE33$; 2) Любая система вида (1*), отражающая функция $IMAGE31$ которая совпадает в области $IMAGE35$ с функцией $IMAGE33$, содержится в рассматриваемом множестве.

Две системы вида (1*), принадлежащие одному классу эквивалентности, будем называть эквивалентными. Допуская определённую вольность речи, будем говорить также, что они имеют одну и ту же отражающую функцию. Функцию $IMAGE33$ при этом будем называть отражающей функцией класса, а класс – соответствующим отражающей функции $IMAGE33$.

Первый интеграл дифференциальной системы и условия его существования

Рассмотрим систему $IMAGE39$= $IMAGE40$  $IMAGE41$  $IMAGE42$(1) с непрерывной в области D функцией f. Дифференцируемая функция U (t, x), заданная в некоторой подобласти G области D, называется первым интегралом системы (1) в области G, если для любого решения x(t), t $IMAGE43$, системы (1), график которого расположен в G функция U (t, x(t)), t $IMAGE43$, постоянна, т.е. U (t, x(t)) зависит только от выбора решения x(t) и не зависит от t.

Пусть V (t, x), V:G $IMAGE45$R, есть некоторая функция. Производной от функции V в силу системы (1) назовем функцию V $IMAGE46$ V $IMAGE47$R, определяемую равенством

$IMAGE48$.

Обозначим V $IMAGE49$ (t, x(t)) $IMAGE50$t $IMAGE43$.

Лемма

Дифференцируемая функция U (t, x), U:G $IMAGE45$R, представляет собой первый интеграл системы (1) тогда и только тогда, когда производная U $IMAGE53$ в силу системы (1) тождественно в G обращается в нуль.

Необходимость. Пусть U (t, x) есть первый интеграл системы (1). Тогда для любого решения x(t) этой системы на основании определения, будем иметь тождества

U $IMAGE54$ $IMAGE55$ $IMAGE56$

Откуда при t=t $IMAGE57$ получим равенство U $IMAGE49$(t $IMAGE59$ справедливое при всех значениях t $IMAGE57$ и x(t $IMAGE57$). Необходимость доказана.

Достаточность. Пусть теперь U $IMAGE62$ при всех (t, x) $IMAGE63$ Тогда для любого решения x(t) системы (1) из определения будем иметь тождества

$IMAGE64$

а с ним и достаточность.

Из определения первого интеграла следует, что постоянная на G функция также является первым интегралом системы (1). По этому первым интегралом на G будем называть функцию $IMAGE65$, для которой выполняется неравенство

$IMAGE66$ и $IMAGE67$

Функцию U(x) будем называть стационарным первым интегралом системы (1), если она не зависит от t и является первым интегралом системы (1).

Возмущения дифференциальных систем, не изменяющие временных симметрий

Наряду с исходной дифференциальной системой

$IMAGE68$  $IMAGE69$  $IMAGE70$  $IMAGE71$

будем рассматривать множество возмущённых систем

$IMAGE72$  $IMAGE69$  $IMAGE70$  $IMAGE75$

где $IMAGE76$непрерывная скалярная нечётная функция, а $IMAGE77$произвольная непрерывно дифференцируемая вектор-функция. Выясним вопрос об эквивалентности в смысле совпадения отражающих функций дифференциальных систем (1) и (2). При совпадении отражающих функций двух систем совпадают их операторы сдвига на симметричном промежутке вида $IMAGE78$ и, значит, для периодических систем совпадают их отображения за период $IMAGE79$.

Как известно, отражающая функция системы (1) обязана удовлетворять соотношению

$IMAGE80$  $IMAGE81$

Если $IMAGE82$ $IMAGE83$вектор-функция, а $IMAGE84$

вектор-столбец, то полагаем

$IMAGE85$  $IMAGE86$, $IMAGE87$

Лемма 1.

Для любых трёх вектор-функций $IMAGE88$  $IMAGE89$  $IMAGE90$ из которых функция $IMAGE91$ дважды непрерывно дифференцируема, а функции $IMAGE92$ и $IMAGE93$ дифференцируемы, имеет место тождество

$IMAGE94$  $IMAGE95$

Лемма 2.

Пусть $IMAGE96$отражающая функция системы $IMAGE71$ с непрерывно дифференцируемой правой частью. Тогда для каждой непрерывно дифференцируемой вектор функции $IMAGE98$ функция

$IMAGE99$  $IMAGE100$

удовлетворяет тождеству

$IMAGE101$

$IMAGE102$  $IMAGE103$

Доказательство. Учитывая соотношение $IMAGE81$, простыми выкладками установим тождества

$IMAGE105$

К первым двум слагаемым последней части этого тождества применим тождество $IMAGE95$. Тогда после несложных формальных преобразований придём к соотношению

$IMAGE107$

$IMAGE108$

Прибавим к левой и правой частям этого соотношения выражение $IMAGE109$ придём к нужному нам тождеству $IMAGE110$

Лемма доказана.

Теорема 1

Пусть вектор-функция $IMAGE98$ является решением дифференциального уравнения в частных производных

$IMAGE112$  $IMAGE113$

Тогда возмущённая дифференциальная система

$IMAGE72$  $IMAGE69$  $IMAGE70$  $IMAGE75$,

где $IMAGE118$- произвольная непрерывная скалярная нечётная функция, эквивалентна дифференциальной системе $IMAGE71$.

Доказательство. Пусть $IMAGE96$отражающая функция системы $IMAGE71$. Следовательно, эта функция удовлетворяет дифференциальному уравнению $IMAGE81$. Покажем, что она удовлетворяет и тождеству

$IMAGE123$  $IMAGE124$

Для этого введём функцию $IMAGE125$ по формуле $IMAGE100$. Согласно лемме 2, эта функция удовлетворяет тождеству $IMAGE103$. При условиях доказываемой теоремы с учётом соотношения $IMAGE128$ это тождество переписывается в виде

$IMAGE82$ $IMAGE130$

Кроме того, поскольку для всякой отражающей функции $IMAGE33$ верно тождество $IMAGE132$, имеет место соотношения

$IMAGE133$.

Таким образом, функция $IMAGE134$ является решением задачи Коши

$IMAGE135$  $IMAGE136$

Решение этой задачи существует и единственно. Следовательно, имеет место тождество $IMAGE137$ влекущее за собой тождество $IMAGE124$.

Теперь покажем, что отражающая функция $IMAGE139$ системы $IMAGE71$ является также и отражающей функцией системы $IMAGE75$. Для этого нужно проверить выполнение основного соотношения $IMAGE81$, которое в данном случае должно быть переписано в виде

$IMAGE143$  $IMAGE144$

Действительно, последовательно преобразовывая левую часть последнего соотношения и учитывая нечётность функции $IMAGE145$ приходим к следующей цепочке тождеств:

$IMAGE146$

Оба слагаемых, стоящих в квадратных скобках, тождественно равны нулю. Первое – в силу того, что для отражающей функции системы $IMAGE71$ верно тождество $IMAGE81$, второе – потому, что при условиях теоремы верно тождество $IMAGE124$. Следовательно, тождество $IMAGE144$ выполняется и функция $IMAGE139$ является отражающей функцией системы $IMAGE75$. Теорема доказана.

А теперь рассмотрим пример.

Пример

Рассмотрим систему

$IMAGE153$

в которой непрерывные и $IMAGE154$периодические функции $IMAGE155$, $IMAGE156$ таковы, что $IMAGE157$ и $IMAGE158$ – нечётные функции.

Эта система эквивалентна стационарной системе

$IMAGE159$

Здесь $IMAGE160$ и $IMAGE161$, $IMAGE162$,

$IMAGE163$.

Так как стационарная система имеет асимптотически устойчивый предельный цикл $IMAGE164$, которому соответствуют $IMAGE154$периодические решения, то из сказанного следует, что все решения $IMAGE166$, $IMAGE167$ рассматриваемой системы, начинающиеся при $IMAGE168$ на окружности $IMAGE169$, являются $IMAGE154$периодическими, а каждое из остальных решений, кроме нулевого, при $IMAGE171$ стремится к одному из указанных периодических.

Общее решение системы

Рассмотрим две дифференциальные системы

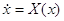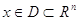,  (1)

$IMAGE6$, $IMAGE7$, 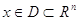, (2)

где $IMAGE177$- непрерывная скалярная нечётная функция, $IMAGE178$-произвольная непрерывно дифференцируемая функция.

Лемма 1

Для любой нечётной функции $IMAGE177$, определённой в окрестности $IMAGE180$, справедливо $IMAGE181$.

Доказательство.

Так как $IMAGE177$- непрерывная нечётная функция, то $IMAGE183$ и

$IMAGE184$ при $IMAGE185$

Лемма 2

Пусть $IMAGE186$ есть первый интеграл системы $IMAGE187$. Тогда $IMAGE188$ есть первый интеграл системы $IMAGE189$.

Доказательство. Т.к. $IMAGE186$ есть первый интеграл системы $IMAGE187$, то его производная в силу системы равна $IMAGE180$, т.е. $IMAGE193$.

Полагая здесь $IMAGE194$, получаем $IMAGE195$  $IMAGE196$, что и означает что $IMAGE197$ первый интеграл системы $IMAGE189$

$IMAGE199$.

Теорема 1.

Пусть $IMAGE200$ – отражающая функция системы $IMAGE189$ и $IMAGE178$удовлетворяет следующему соотношению 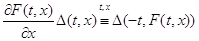 (3)

Тогда система $IMAGE187$ эквивалентна системе $IMAGE189$ в смысле совпадения отражающих функций.

Доказательство. Поскольку $IMAGE200$ отражающая функция системы $IMAGE189$, то $IMAGE208$  $IMAGE82$(4). Рассмотрим выражение $IMAGE210$

$IMAGE211$(равно $IMAGE180$ т.к. $IMAGE33$ отражающая функция системы $IMAGE214$)+ $IMAGE215$(равно $IMAGE180$ по $IMAGE217$) $IMAGE218$ (4)

$IMAGE219$означает, что $IMAGE220$отражающая функция системы $IMAGE187$. Поскольку у систем $IMAGE189$ и $IMAGE187$отражающие функции совпадают, то системы $IMAGE189$ и $IMAGE187$эквивалентны в смысле совпадения отражающих функций.

Введём такие обозначения $IMAGE195$

$IMAGE227$ и $IMAGE228$- семейства функций, являющиеся решениями систем $IMAGE187$ и $IMAGE189$, соответственно $IMAGE231$ и $IMAGE232$- решение систем $IMAGE187$ и $IMAGE189$ соответственно.

Лемма 4

Пусть $IMAGE235$ первый интеграл системы $IMAGE189$. Если выполнено соотношение $IMAGE237$ (5), где $IMAGE238$некоторая функция, то $IMAGE239$ есть первый интеграл системы $IMAGE187$, где $IMAGE241$.

Доказательство. Так как $IMAGE241$, то $IMAGE243$ удовлетворяет уравнению $IMAGE244$, так как $IMAGE245$, то $IMAGE246$. Умножим обе части справа на 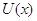, получим $IMAGE248$. Перенесём всё в левую часть и к левой части прибавим выражение $IMAGE249$. Так как 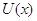- первый интеграл, получим $IMAGE251$. Т.е. производная функции $IMAGE239$ в силу системы $IMAGE18