Содержание
Глава 1. Введение в дифференциальную геометрию поверхностей. Основные понятия
1.1 Первая квадратичная форма поверхности
1.2 Внутренняя геометрия поверхности
1.3 Вторая квадратичная форма поверхности
1.4 Классификация точек регулярной поверхности
1.5 Средняя и гауссова кривизны поверхности
Глава 2. Понятие поверхности Каталана
2.1 Общие положения
2.2 Примеры поверхностей Каталана
2.3 Виды поверхностей Каталана
Глава 3. Дифференциальная геометрия поверхностей Каталана
3.1 Первая и вторая квадратичные формы линейчатой поверхности
3.2 Первая и вторая квадратичные формы поверхности Каталана
3.3 О коноидах
Глава 4. Специальные поверхности Каталана (поверхности класса КА)
4.1 Вывод уравнения поверхности класса КА
4.2 Вывод уравнения поверхности класса КА по заданным кривым и нормальному вектору порождающей плоскости
Глава 5. Дифференциальная геометрия поверхностей класса КА
5.1 Первая и вторая квадратичные формы линейчатой поверхности
5.2 Первая квадратичная форма поверхности класса КА
5.3 Вторая квадратичная форма поверхности класса КА
Глава 6. О программе визуализации и анализа поверхностей
6.1 Общие положения и возможности программы
6.2 Примеры работы
Выводы
Список литературы
Глава 1. Введение в дифференциальную геометрию поверхностей.
Основные понятия
1.1 Первая квадратичная форма поверхности
Пусть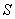 
- гладкая поверхность, 
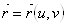– ее векторное параметрическое уравнение и 
.
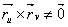Определение 1.1.
Первой квадратичной формой на поверхности 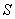называется выражение
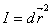(1)
Распишем это выражение подробнее.
$IMAGE6$,
$IMAGE7$
Откуда $IMAGE8$ (2)
Выражение (2) в каждой точке поверхности 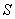представляет собой квадратичную форму от дифференциалов $IMAGE10$ и $IMAGE11$. Первая квадратичная форма является знакоположительной, так как ее дискриминант
$IMAGE12$ и $IMAGE13$.
Для коэффициентов первой квадратичной формы часто используют следующие обозначения (и мы в своих исследованиях будем придерживаться именно их) ([1].[2],[3]):
$IMAGE14$,
$IMAGE15$,
$IMAGE16$.
Так что выражение (2) для формы $IMAGE17$ можно переписать в виде
$IMAGE18$ (3)
Соответственно,
$IMAGE19$.
1.2 Внутренняя геометрия поверхности
Известно, что, зная первую квадратичную форму поверхности, можно вычислять длины дуг кривых на поверхности, углы между кривыми и площади областей на поверхности. В самом деле, если рассмотреть формулы, определяющие вышеуказанные величины, можно заметить, что туда входят только лишь коэффициенты $IMAGE20$, $IMAGE21$, $IMAGE22$ первой квадратичной формы. Поэтому если известная первая квадратичная форма поверхности, можно исследовать геометрию на поверхности, не обращаясь к ее уравнениям, а лишь используя ее первую квадратичную форму.
Совокупность геометрических фактов, относящихся к поверхности, которые можно получить при помощи ее первой квадратичной формы, составляет так называемую внутреннюю геометрию поверхности.
Поверхности, имеющие одинаковые первые квадратичные формы и потому имеющие одинаковую внутреннюю геометрию, называются изометричными.
Рассмотрим простой пример.
Пусть задана поверхность
$IMAGE23$
Это цилиндрическая поверхность с синусоидой в качестве направляющей.
$IMAGE24$
Имеем:
$IMAGE25$, $IMAGE26$
Поэтому
$IMAGE27$,
$IMAGE28$,
$IMAGE29$
Следовательно,
$IMAGE30$.
Если сделать замену, вводя новые параметры $IMAGE31$ и $IMAGE32$ таким образом
$IMAGE33$,
$IMAGE34$.
Тогда первая квадратичная форма поверхности примет, очевидно, вид
$IMAGE35$.
Мы видим, что в новых переменных первая квадратичная форма рассматриваемой цилиндрической поверхности совпадает с первой квадратичной формой плоскости $IMAGE36$ и поэтому внутренняя геометрия этой поверхности совпадает с внутренней геометрией плоскости. Т.е. синусоидальный цилиндр изометричен плоскости. Этот важный факт мы еще получим несколько другим способом.
Чисто геометрически это свойство понятно: синусоидальный цилиндр получается изгибанием (т.е. деформацией без сжатий и растяжений) обычной плоскости. При такой деформации внутренняя геометрия не изменяется.
Более того, можно показать, что если одна поверхность получается из другой путем изгибания, то внутренние геометрии этих поверхностей совпадают.
1.3 Вторая квадратичная форма поверхности
1.3.1. Определение второй квадратичной формы.
Основным объектом рассмотрения в этой части изложения станет $IMAGE37$ - регулярная поверхность 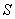, заданная своим радиус-вектором.
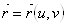, $IMAGE40$
В каждой точке такой поверхности помимо единичного вектора нормали
$IMAGE41$ (1)
Определен и второй дифференциал радиус вектора
$IMAGE42$ (2)
Определение 1.2.
Второй квадратичной формой поверхности 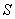называется скалярное произведение векторов $IMAGE44$ и $IMAGE45$.
$IMAGE46$ ([1],[3],[4],[5]) (3)
Нетрудно заметить, что в каждой точке поверхности 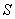квадратичная форма (3) является квадратичной формой относительно дифференциалов $IMAGE10$ и $IMAGE11$.
Для коэффициентов второй квадратичной формы приняты (и мы также в дальнейшем будем пользоваться этим) следующие обозначения
$IMAGE50$ (4)
Это позволяет записать ее в следующем простом виде
$IMAGE51$ (5)
Покажем еще один способ вычисления коэффициентов второй квадратичной формы поверхности.
Заменим в формулах (4) единичный вектор нормали $IMAGE45$ на его выражение (1), получим,
$IMAGE53$ (6)
Для подробного вывода нужно знать тождество:
$IMAGE54$.
Продолжим рассуждения.
Так как векторы $IMAGE6$ и $IMAGE45$ ортогональны (первый, разумеется лежит в касательной плоскости к поверхности, а второй лежит в плоскости нормального сечения).
Поэтому
$IMAGE57$.
Откуда
$IMAGE58$
Отсюда, дифференцируя, получим:
$IMAGE59$ (7)
Это дает еще один способ расчета второй квадратичной формы.
$IMAGE60$([5],[6]) (8)
Отсюда же можно получить новые формулы для вычисления коэффициентов второй квадратичной формы. Впрочем, удобнее продифференцировать по $IMAGE61$ и по $IMAGE62$ очевидные равенства
$IMAGE63$ и $IMAGE64$.
Воспользовавшись соотношениями (4), получаем, что
$IMAGE65$ (9)
Вторая квадратичная форма эффективна при выяснении графических свойств регулярной поверхности.
1.4 Классификация точек регулярной поверхности
Пусть 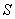– регулярная поверхность и 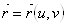– ее параметрическое задание.
Выберем на поверхности некоторую точку $IMAGE69$ и рассмотрим плоскость $IMAGE70$, которая касается поверхности в этой точке.
Отклонение произвольной точки $IMAGE31$ поверхности от плоскости $IMAGE70$ определим по формуле
$IMAGE75$ (1)
В этой формуле $IMAGE76$ – единичный вектор нормали к поверхности в точке $IMAGE77$. Это отклонение, взятое по абсолютной величине, равно расстоянию от точки $IMAGE31$ до плоскости $IMAGE70$. Отклонение положительно, если точка $IMAGE31$ и конец вектора $IMAGE76$ лежат по одну сторону от касательной плоскости, соответственно, оно отрицательно, если они лежат по разные стороны от касательной плоскости в точке $IMAGE77$.
Рассмотрим формулу (1).
Разность $IMAGE83$ допускает следующую интерпретацию
$IMAGE84$ (2)
Где
$IMAGE85$, при $IMAGE86$.
Умножим обе части равенства (2) скалярно на вектор $IMAGE76$ и положив
$IMAGE88$, $IMAGE89$.
Получим, что
$IMAGE90$ (3)
Разумеется, вдумчивый (или хотя бы немного читающий эти выкладки) читатель поймет, что коэффициенты
$IMAGE91$,
$IMAGE92$,
$IMAGE93$
указанные в формуле (3) вычислены в точке $IMAGE77$, в окрестности которой мы и рассматриваем исходную поверхность .
Из курса линейной алгебры известно, что свойства квадратичной формы во многом определяются ее дискриминантом. А скорее даже знаком квадратичной формы.
Вычислим дискриминант второй квадратичной формы в точке $IMAGE77$.
$IMAGE97$
Рассмотрим все возможные случаи.([7],[8],[9],[10],[11])
Случай 1.
$IMAGE98$
Т.е. вторая квадратичная форма поверхности в заданной точке является знакоопределенной.
Зафиксируем в точке $IMAGE77$ некоторое направление на поверхности. Пускай $IMAGE100$.
Тогда любое другое направление на поверхности в точке $IMAGE77$ можно задавать при помощи угла $IMAGE102$, который оно образует с уже выбранным направлением.
Положим
$IMAGE103$, $IMAGE104$
Тогда
$IMAGE105$ (4)
Нетрудно показать, что
$IMAGE106$,
где постоянная
$IMAGE107$
а в силу условия
$IMAGE98$ положительна.
Таким образом неравенство
$IMAGE109$
выполняется независимо от выбора угла $IMAGE102$.
Так как порядок стремления к нулю при $IMAGE111$ второго слагаемого $IMAGE112$ в правой части формулы (3) выше двух, то из последней оценки можно сделать следующий вывод.
Отклонение $IMAGE113$ сохраняет знак (совпадающий со знаком второй квадратичной формы $IMAGE114$) для всех достаточно малых значений $IMAGE115$независимо от выбора направления на поверхности.
Это означает, что все точки поверхности , достаточно близкие к точке $IMAGE77$, располагаются по одну сторону от касательной плоскости поверхности в этой точке. Такая точка поверхности называется эллиптической точкой.
Например, все точки сфер – эллиптические.([6],[8])
$IMAGE119$
Случай 2.
$IMAGE120$.
Вторая квадратичная форма является знакопеременной.
Покажем, что в этом случае, в точке $IMAGE77$ можно указать два неколлинеарных направления на поверхности, обладающие следующими свойствами:
- для значений дифференциалов, определяющих эти направления, вторая квадратичная форма поверхности, вычисленная в точке $IMAGE77$, обращается в нуль,
- все остальные направления на поверхности в точке $IMAGE77$ разбиваются на два класса – для дифференциалов, определяющих направления одного из этих классов, вторая квадратичная форма положительна и для другого отрицательна.
Пусть некоторое направление $IMAGE124$ положительного класса задается углом $IMAGE102$. В соответствии с формулой (4) имеем
$IMAGE126$, ([1],[4],[11])
где $IMAGE127$
Как видно из формулы (3), знак отклонения $IMAGE113$ для всех достаточно малых значений $IMAGE115$ в рассматриваемом направлении $IMAGE102$ совпадает со знаком второй квадратичной формы $IMAGE114$. Следовательно, если точка $IMAGE31$ поверхности достаточно близка к точке $IMAGE77$, то это отклонение положительно.
Рассуждая аналогично, можно указать точки на поверхности, близкие к точке $IMAGE77$, для которых отклонение $IMAGE113$ будет отрицательным.
Приведенные рассуждения показывают, что вблизи точки $IMAGE77$ поверхность располагается по разные стороны от касательной плоскости. При этом проекции точек поверхности, отклонения которых расположены на касательный плоскости заполняются множество «между» этими направлениями…
В этом случае точка называется гиперболической точкой поверхности.
$IMAGE139$
Случай 3.
$IMAGE140$.
Но отличен от нуля хотя бы один из коэффициентов, $IMAGE141$, $IMAGE142$.
Пусть для определенности $IMAGE143$. Тогда вторая квадратичная форма поверхности 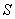в точке $IMAGE77$ мо