Численные методы вычисления интегралов. Метод Ньютона-Котеса. Метод Гаусса
1. Численные методы вычисления интегралов. Постановка задачи
Решая физические задачи, часто приходится вычислять значения определённых интегралов от функций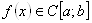 
. Во многих случаях, в виду того, что подлежащий вычислению интеграл не выражается через элементарные функции, прибегают к приближённым численным методам.
Прежде всего, рассмотрим случай, когда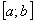 
- конечный интервал.
В таком случае, как известно, функция 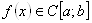является ограниченной, т.е. 
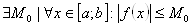. В этом случае наиболее часто применяемый численный метод интегрирования состоит в том, что интеграл от 
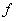заменяется некоторой линейной комбинацией значений $IMAGE6$ в $IMAGE7$ точках $IMAGE8$:
$IMAGE9$(1)
Формула (1) называется квадратурной формулой, а коэффициенты $IMAGE10$ - квадратурными коэффициентами или весами, абсциссы $IMAGE11$ - узлами квадратурной формулы.
Методы численного интегрирования классифицируются в зависимости от того, заданы ли значения аргумента через равные промежутки или нет. Так методы Ньютона-Котеса требуют, чтобы значения $IMAGE12$ были заданы с постоянным шагом, а методы Гаусса не налагают такого ограничения. Перейдём к рассмотрению этих методов.
2. Методы Ньютона-Котеса
Пусть $IMAGE13$ различные точки отрезка 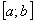, служащие узлами интерполяции для некоторой интерполирующей функцию $IMAGE15$ функции $IMAGE16$. Тогда имеем:
$IMAGE17$(2)
где $IMAGE18$ - остаточный член. Предположим, что
$IMAGE19$(3)
причём $IMAGE20$ подобраны так, чтобы все интегралы
$IMAGE21$(4)
можно вычислить точно. Тогда мы получаем квадратурную формулу
$IMAGE9$ (5)
2.1 Формула трапеций
Частным случаем методов Ньютона-Котеса является квадратурная формула трапеции. Подынтегральную функцию будем интерполировать по формуле Лагранжа, в том случае, когда на каждом отрезке деления принимается линейная интерполяция, а результаты суммируются (рис 1):
$IMAGE25$
Рис. 1.
а) графический вывод:
Определённый интеграл $IMAGE26$, как известно, задаёт площадь $IMAGE27$ криволинейной трапеции $IMAGE28$, поэтому, вписав ломаную в дугу кривой $IMAGE29$, мы получаем, что площадь криволинейной трапеции можно приближённо вычислить как сумму площадей трапеций:
$IMAGE30$(6)
Между тем, очевидно, что
$IMAGE31$(7)
Так как, в методах Ньютона-Котеса, $IMAGE32$, учитывая (6) получаем:
$IMAGE33$ (8)
или, соединяя подобные члены, имеем:
$IMAGE34$ (9)
Формула (9) – называется формулой трапеций.
б) Аналитический вывод:
Выведем формулу трапеции аналитическим способом. Для этого используем интерполяционный многочлен Лагранжа для отрезка $IMAGE35$, построим многочлен первой степени, который на концах отрезка принимает заданные значения $IMAGE36$. Ясно, что в таком случае интерполирующая функция $IMAGE37$ имеет вид:
$IMAGE38$(10)
т.к. в методе Ньютона-Котеса $IMAGE39$, учитывая (3) и (4), из (10) получаем:
$IMAGE40$
$IMAGE41$ (11)
Аналогично, $IMAGE42$, т.е.
$IMAGE43$ (12)
Таким образом, получаем формулу:
$IMAGE44$ (13)
тогда, используя свойство аддитивности оператора интегрирования, имеем:
$IMAGE45$ (14)
где $IMAGE46$. Получили формулу (14) трапеций, которая естественно, совпадает с (9).
2.2 Формула Симпсона
Рассмотрим метод Ньютона-Котеса (т.е. $IMAGE39$), в случае интерполяции подинтегральной функции квадратичными функциями на каждом интервале деления. В данном случае мы имеем дело с параболическим интерполированием, поэтому на каждом интервале $IMAGE48$, необходимо знание значения функции $IMAGE49$ в трёх точках (т.к. $IMAGE50$ имеет 3 неизвестных параметра – коэффициенты $IMAGE51$). В качестве третьей точки на каждом отрезке $IMAGE52$ - выбирается середина этого отрезка, т.е. точка $IMAGE53$.
Вывод формулы Симпсона будем производить аналитически. Как и в предыдущем случае применяем интерполяционный многочлен Лагранжа, для интерполирования функции $IMAGE49$, на отрезке $IMAGE48$, при чём считаем, что нам известны значения $IMAGE56$. Тогда, очевидно, что многочлен Лагранжа имеет вид квадратичной функции:
$IMAGE57$ (15)
Интегрируя (15) на отрезке $IMAGE52$ будем иметь формулу:
$IMAGE59$(16)
используя свойство аддитивности интеграла, получаем:
$IMAGE60$(17)
где $IMAGE61$является четным числом ( $IMAGE61$- число делений отрезка 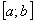,т.е. число равных отрезков разбиения).
Формула (17)-называется формулой Симпсона.
Приняв обозначения $IMAGE64$, получаем привычный вид квадратурных формул:
а) Формула трапеций:
$IMAGE65$(18)
б) Формула парабол (Симпсона) (при $IMAGE66$)
$IMAGE67$(19)
2.3 Метод Ромберга
Пусть промежуток интегрирования разбит на $IMAGE68$ равных частей и для этого разбиения по формуле трапеции получено значение $IMAGE69$. Значение $IMAGE69$ - совпадает со значением вычисляемого интеграла, если интегрируемая функция $IMAGE71$ линейна, т.е. является многочленом первой степени. По формуле:
$IMAGE72$(20)
называемой формулой Ромберга, построим $IMAGE73$- схему:
$IMAGE74$(21)
Оказывается, что для интегрируемых по Риману функций, все столбцы и строки $IMAGE73$- схемы сходятся к исходному значению интеграла.
Пример: Выписать явные формулы для фрагмента $IMAGE73$- схемы:
$IMAGE77$
$IMAGE78$
$IMAGE79$ $IMAGE80$
$IMAGE81$
$IMAGE82$
Решение:
Пусть $IMAGE83$Тогда
$IMAGE84$
$IMAGE85$
$IMAGE86$
$IMAGE87$
$IMAGE88$
$IMAGE89$
3. Квадратурные формулы Гаусса
Во всех приведенных до сих пор формулах численного интегрирования Ньютона-Котеса и во всех формулах, получаемых методом Ромберга, используются равноотстоящие узлы. В случае квадратурных формул Гаусса это уже не так. Иначе говоря, смысл квадратурных формул Гаусса состоит в том, чтобы при наименьшем возможном числе узлов точно интегрировать многочлены наивысшей возможной степени. Можно показать, что при $IMAGE90$гауссовых узлах по полученной формуле можно точно интегрировать многочлены степени $IMAGE91$.
$IMAGE92$(22)
Для количества узлов и соответствующих значений $IMAGE93$и $IMAGE94$- составлены таблицы, которые позволяют вычислять интегралы по формуле (22).
Для понимания сути этих таблиц рассмотрим пример.
Пример:
Пусть нам нужно составить квадратурную формулу с двумя узлами $IMAGE95$,по которой точно интегрируются многочлены до $IMAGE96$степень включительно.
Решение: Искомая формула имеет вид:
$IMAGE97$,(23)
где $IMAGE98$ - остаток, который обращается в нуль, для
$IMAGE99$, при $IMAGE100$.
Тогда, подставляя в (23) имеем:
$IMAGE101$(24)
Отсюда, приравнивая коэффициенты при $IMAGE102$ $IMAGE103$, справа и слева, получаем систему уравнений:
$IMAGE104$(25)
Ее решение имеет вид:
$IMAGE105$(26)
Следовательно, искомая квадратурная формула такова:
$IMAGE106$.(27)
Ясно, что если нам нужно вычислить интеграл со многими узловыми точками, действуем следующим образом:
а) промежуток интегрирования $IMAGE107$ делим на $IMAGE61$- равных промежутков и на каждом маленьком промежутке $IMAGE35$ применяем формулу Гаусса с неравноотстоящими узлами (27);
б) полученные результаты складываем.
В случае, когда $IMAGE110$, оказывается, что узловыми точками при делении отрезка на $IMAGE61$- частей являются корни соответствующих многочленов Лежандра.
Для вычисления кратных интегралов, их сводят обычно к повторным интегралам, а далее применяют те же самые кубатурные формулы для каждого значения узловых точек, что и в одномерном случае. Однако, надо иметь в виду, что кратные интегралы значительно сложнее вычислять с заданной точностью.
Точность произведённых вычислений зависит от точности аппроксимации подынтегральной функции многочленами.
4. Оценка интегралов
При численном интегрировании наряду с приближёнными формулами представляет также интерес нахождение нижних и верхних границ интегралов. Рассмотрим два метода оценки интегралов:
а) оценка интеграла в случае, когда подинтегральная функция $IMAGE49$, удовлетворяет условию:
$IMAGE113$ для $IMAGE114$ (28)
б) общий случай.
Рассмотрим интеграл:
$IMAGE115$ (29)
где $IMAGE113$, $IMAGE114$. Не умоляя общность, будем считать, что $IMAGE118$, $IMAGE114$, тогда (Рис. 1) ясно, что
$IMAGE120$ $IMAGE121$ $IMAGE122$ $IMAGE122$ $IMAGE124$ $IMAGE125$ $IMAGE126$ $IMAGE127$ $IMAGE128$ $IMAGE129$
К Е
N
М
0 $IMAGE130$ $IMAGE131$ $IMAGE132$ $IMAGE12$
Рис. 1
0 $IMAGE130$ $IMAGE131$ $IMAGE132$ $IMAGE12$
Площадь криволинейной трапеции $IMAGE138$ заключена между площадями aMNb и aKEb, т.е.
$IMAGE139$(30)
Очевидно, что
$IMAGE140$(31)
$IMAGE141$(32)
Таким образом, для оценки интеграла в случае $IMAGE142$, имеем:
$IMAGE143$(33)
если же $IMAGE144$, неравенство (33) заменяется на обратное.
б) Другой принцип грубой, но зато общей оценки значения интеграла, основан на «монотонности» интеграла. При этом способе подынтегральную функцию приближают снизу и сверху интегрируемыми в замкнутом виде функциями $IMAGE145$ и $IMAGE146$, т.е.
$IMAGE147$, $IMAGE148$(34)
Тогда
$IMAGE149$(35)
5. Вычисление интегралов методом Монте-Карло
Пусть нам нужно вычислить интеграл:
$IMAGE150$(36)
В случае, когда методы Ньютона-Котеса и Гаусса работают плохо, приходится обращаться к вероятностным методам случайного поиска. К таким методам относится метод Монте-Карло.
Для вычисления интеграла (36) методом Монте-Карло, заменим переменную интегрирования $IMAGE151$ таким образом, чтобы пределы интегрирования 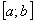отобразились соответственно в $IMAGE153$. Для этого нужно воспользоваться преобразованием:
$IMAGE154$(37)
тогда интеграл (36) принимает вид:
$IMAGE155$(38)
Для вычисления же интеграла на $IMAGE153$ имеем формулу:
$IMAGE157$(39)
где $IMAGE158$ - случайные числа, равномерно распределённые на $IMAGE153$. Таким образом, по методу Монте-Карло, интеграл (36) считается по формуле:
$IMAGE160$(40)
где $IMAGE158$ - равномерно распределённые случайные числа из промежутка $IMAGE153$.
Аналогично, для кратных интегралов. Получаем:
$IMAGE163$(41)
где $IMAGE164$ - случайные точки, равномерно распределённые на квадрате $IMAGE165$ (Здесь знак « $IMAGE12$» означает декартовое произведение).
В случае, когда область интегрирования является сложным множеством $IMAGE167$ (рис. 6), пользуемся прямоугольником $IMAGE168$, который описывается вокруг множества $IMAGE167$. И интеграл по множеству $IMAGE167$ заменяем интегралом по прямоугольнику $IMAGE168$, который уже умеем вычислять по формуле (41). Замена интеграла по множеству $IMAGE167$ производится соотношением:
$IMAGE173$ (42)
где
$IMAGE174$ (43)
таким образом:
$IMAGE175$ (44)
который легко рассчитывается по формуле (41).
Аналогично вычисляются и трёхкратные ин