ЛЕКЦИЯ №1
Численные методы представляют собой набор алгоритмов, позволяющих получать приближенное (численное) решение математических задач.
Погрешности, возникающие при решении задач, бывают двух видов:
1)абсолютная

 p - p
p - p  , где p - точное значение, p - не точное.
, где p - точное значение, p - не точное.
2)относительная
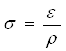
Эмпирические данные:
| | | | | |
| |  |
| $IMAGE6$ | | $IMAGE7$ |
|
|
Погрешности Случайные Ошибки
измерительного помехи набора
прибора
1) Нахождение нулей функции;
2) Системы линейных и нелинейных уравнений;
3) Приближение функции. Интерполяция. Экстраполяция.
4) Решение дифференциальных уравнений.
5) Расчет собственных значений и собственных векторов матриц.
НАХОЖДЕНИЕ НУЛЕЙ ФУНКЦИИ
Общая постановка задачи
Дана некоторая функция f(х). Необходимо найти хотя бы одно значение х, при котором f(х)=0.
Этапы:
1) Отделение корней.
Область определения функции разбивается на отрезки, на каждом из которых
содержится единственный корень функции.
2) Уточнение корня при помощи одного из численных методов на каждом из выбранных отрезков.
Нуль функции – точка пересечения графика функции с осью Ох.
Непрерывность f(х) в точке х0:
$IMAGE8$
Производная функции: f' = $IMAGE9$ $IMAGE10$
Физический смысл: f'(х0)- скорость
Геометрический смысл: f'(х0)-тангенс угла наклонной касательной к графику функции, проведенной в данной точке.
Если функция дифференцируема в точке, то она непрерывна. Обратное не верно.
Предел функции в точке: $IMAGE11$
$IMAGE12$x: | x-x0| < $IMAGE13$
$IMAGE12$ε >0 $IMAGE15$(ε)
| f(x) – A| < ε
Градиент функции – это вектор.
$IMAGE16$
Геометрический смысл : показывает направление локального возрастания функции в данной точке .
$IMAGE17$
1) Наблюдаем смену знака функции.
2) Исследуем функцию на монотонность.
Теорема №1: если функция f(x) непрерывна на отрезке [a, b] и в концах отрезка принимает значения разных знаков, то на этом отрезке функция имеет хотя бы один корень.
f(x) $IMAGE18$ C[a, b]
f(a) * f(b) < 0 → $IMAGE19$ $IMAGE20$ $IMAGE18$[a, b] f( $IMAGE20$)=0
Теорема№2: если функция непрерывна и монотонна на отрезке и в концах отрезка принимает значения разных знаков, то на этом отрезке существует только единственный корень функции.
$IMAGE23$ $IMAGE24$f(x) $IMAGE18$C[a, b], f ( ) и f(a) * f(b) < 0→ $IMAGE19$ $IMAGE20$ $IMAGE18$[a, b] f( $IMAGE20$) = 0
МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ
$IMAGE30$
Дано: f(x) непрерывна на [a,b], на [a,b] существует динственный корень f(x)=0, ε
1) Делим отрезок пополам. Получаем точку
с= (b + a)/2.
Если f(a) * f(c) < 0,то b:=c.
Если f(b) * f(c) < 0,то а:=с
2) Продолжаем делить [a, b] на 2, пока|b-a| > ε, где ε- заданная точность.
ЛЕКЦИЯ №2
МЕТОД ХОРД
Дано: 1) f(x) $IMAGE31$ C''[a, b]
2) f(a) * f(b) < 0
3) f'(x) и f''(x) знакопостоянна на отрезке [a, b].
4) ε, чтобы получить f(x)=0
$IMAGE32$
1) f(b) 2)
f'(x) >
0 f'(x) > 0
f''(x) >
0 f''(x) < 0
$IMAGE33$ f(a) a x
$IMAGE34$ 3) 4)
f'(x)
<0 f'(x) <0
f''(x)
<0 f''(x) > 0
$IMAGE35$ (2.1)
x1(x1,f(x1))
$IMAGE36$
b – неподвижный конец отрезка.
Для случаев 1), 3)
$IMAGE37$
Для случаев 2), 4)
$IMAGE38$
Можем ввести некоторую с:
$IMAGE39$ (2.2)
$IMAGE40$ (2.3)
Алгоритм:
1) Вычисляем неподвижный конец отрезка секущих по формуле(2.3)
2) Находим первое приближение к корню по формуле (2.1)
3) Находим первое приближение к корню по формуле (2.2) до тех пор, пока модуль разности двух последних приближений не станет меньше заданной точности. В этом случае, значением корня является последнее приближение.
МЕТОД КАСАТЕЛЬНЫХ
Дано: 1) f(x) $IMAGE31$ C''[a, b];
2) f(a)*f(b) < 0;
3) f'(x) и f''(x) знакопостоянны на [a, b];
4) ε, чтобы решить уравнение f(x)=0
$IMAGE42$
$IMAGE43$
т. х0
y=f(x0)+f'(x0)(x-x0) –
уравнение касательной
a x2 x1 b
y=f(b)+f’(b)*(x-b)
(x1,0) : 0= f(b)+ f’(b)(x1-b)
x1= $IMAGE44$
x2= $IMAGE45$
xn+1= $IMAGE46$ (2.4)
Второй подход (метод Ньютона):
$IMAGE47$-приближение
0 = f( $IMAGE48$) = f(xn+hn) ≈ f(xn)+f'(xn)*hn
x0 = $IMAGE49$ начальное приближение (2.5)
Алгоритм:
1) По формуле (2.5) находим первое приближение к корню х0 (начальное)
2) По формуле (2.4) находим последующее приближение к корню до тех пор, пока модуль разности двух последних приближений не станет заданной точности. В этом случае корень равен последнему приближению.
МЕТОД ИТЕРАЦИЙ
Дано: 1) f(x) $IMAGE31$C''[a,b]
2)f(a)*f(b)<0
3)f'(x) знакопостоянна
4)ε, f(x)=0
Уравнение f(x)=0 заменяется уравнением вида x=φ(x)
φ(x)=x-f(x)*C (2.6)
$IMAGE51$ Пока |xn+1-xn|<ε
φ' >0
Cтроим последователь $IMAGE52$
Выбираем $IMAGE53$
Находим значение функции
x2= φ(x1), x3= φ(x2)
xn+1= φ(xn) (2.7)
Точка ε, для которой выполняется ε=f(ε), называется неподвижной точкой метода итераций. Очевидно, что эта точка является корнем уравнения f(x)=0.
φ(ε) $IMAGE54$ ε -f(x)* ε
0 $IMAGE54$f(ε)*C
f(ε) $IMAGE54$0
Достаточное условие: для того, чтобы метод итераций сходился достаточно чтобы:
1) φ(x) $IMAGE57$ (2.8) - Функция является непрерывной и дифференцируемой на [a,b].
2) φ(x) значения $IMAGE58$ - является необходимым условием
3) |φ(x)|<1 для всех $IMAGE59$
Константа С в формуле(2.6) подбирается таким образом, чтобы функция
φ(x) удовлетворяла условиям сходимости метода итераций.
Скорость сходимости метода Ньютона (касательных) выше сходимости метода секущих (хорд).
ЛЕКЦИЯ №3
МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Общий вид алгебраического уравнения:
а0хn+ а1хn+1+…+ аn-1х+an=0, a0 $IMAGE60$0 (3.1)
n=1: а0х+a1=0, x= $IMAGE61$
n=2: а0х2+a1x+a2=0, x1,2= $IMAGE62$
Алгебраическое уравнение n- степени имеет ровно n корней.
Теорема Виета (обобщенная):
xn+ $IMAGE63$xn-1+…+ $IMAGE64$x+ $IMAGE65$=0
x1+x2+…+xn=- $IMAGE63$; (3.2)
x1x2+x1x3+…+xn-1xn= $IMAGE67$;
x1x2x3…xn=(-1) $IMAGE65$;
Пусть все корни уравнения (3.1) действительны, различны и удовлетворяют соотношениям:
|x1|>>|x2|>>…>>|xn| (3.3)
Преобразуем:
$IMAGE69$x1(1+ $IMAGE70$+…+ $IMAGE71$)= $IMAGE63$ $IMAGE73$ x1=- $IMAGE63$; (3.4)
Подставим (3.4) : х2=- $IMAGE75$ продолжая получим общую формулу
хk=- $IMAGE76$, k=1,n (3.5)
Корни уравнения, удовлетворяющие соотношения(3.3), называются отдельными. Задача состоит в том, чтобы по исходному уравнению построить такое уравнение, корни которого будут отделены.
yi=-xim
b0yn + b1yn-1+…+ bn-1y+bn=0 (3.6)
|x1|>|x2|>…>|xn|
Решив уравнение (3.6), корни которого являются отдельными, получим уравнения y1…yn
$IMAGE77$, i=2,n
Значит |yi-1|>>|xi|
МЕТОД ЛОБАЧЕВСКОГО
Для отделения корней Лобачевский предложил метод квадратирования - способ построения по исходному уравнению нового уравнения, кони которого связаны с корнями исходного следующим образом:
yi=-xi2 (3.7)
Процедура выполнения многократна, пока не достигнем серьёзной разницы модуля разности корней
b0(m)yn + b1(m)yn-1+…+ bn-1(m)y+ bn(m)=0 (3.8)
Пусть уравнение (3.8) получено в результате m-го шага квадрирования.
m=1 b0(1)=a02, b1(1)= a12=2 a0 a2
bk(1)=ak2-2ak-1ak+1+2ak-2ak+2….,k=0,n
При получении bk коэффициента , который рассчитывается как квадрат соответствующего коэффициента ak минус удвоенное произведение соседних коэффициентов с ak плюс удвоенное произведение следующей пары соседей , чередуя знаки, пока в число соседних коэффициентов не попадут а0 и аn.
$IMAGE78$m>1b0(m)=( b0(m-1))2, b1(m)=( b1(m-1))2-2b0(m-1)b2(m-1) (3.9)
bk(m)=( b0(m-1))2-2bk-1(m-1)bk-1(m-1)+2bk-2(m-1)bk+2(m-1)
Критерий остановки: bk(m)≈( b0(m-1))2, k=0,n (3.10)
Получим корень: yi(m)