МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
"Гомельский государственный университет
имени Франциска Скорины"
Математический факультет
Кафедра алгебры и геометрии
Курсовая работа
БИПРИМАРНЫЕ ГРУППЫ
Исполнитель:
студентка группы H.01.01.01 М-33
Стародубова Н.С.
Научный руководитель:
доктор физико-математических наук,
профессор кафедры Алгебры и геометрии
Монахов В. С.
Гомель 2003
Содержание
Введение
1.Основные обозначения
2. Разрешимость факторизуемой группы с разложимыми факторами
3. О произведении 2-разложимой группы и группы Шмидта
4. Произведение бипримарной и 2-разложимой групп
5. Произведение бипримарной и примарной групп
6. Доказательство теоремы (3)
Заключение
Список литературы
Введение
В данной курсовой работе приводятся свойства конечных групп, являющихся произведением двух групп, а именно являющихся произведением двух групп, одна из которых группа Шмидта, а вторая 2-разложимая, произведением бипримарной и 2-разложимой групп.
В третьем пункте данной курсовой работы доказываются следующие теоремы:
Теорема. Пусть  и
и  --- подгруппы конечной группы
--- подгруппы конечной группы  и пусть
и пусть 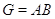 . Если подгруппы
. Если подгруппы  и
и  $IMAGE7$-разложимы для каждого $IMAGE8$, то
$IMAGE7$-разложимы для каждого $IMAGE8$, то  разрешима.
разрешима.
Теорема. Пусть  и
и  --- подгруппы конечной группы
--- подгруппы конечной группы  и пусть
и пусть 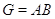 . Предположим, что
. Предположим, что  и
и  --- $IMAGE7$-замкнуты для каждого $IMAGE17$. Если
--- $IMAGE7$-замкнуты для каждого $IMAGE17$. Если  и
и  $IMAGE20$-разложимы и $IMAGE21$-разложимы, то
$IMAGE20$-разложимы и $IMAGE21$-разложимы, то  разрешима.
разрешима.
В четвертом пункте доказазываются приведенные ниже теоремы.
Теорема. Пусть  есть группа Шмидта,
есть группа Шмидта,  --- 2-разложимая группа, порядки
--- 2-разложимая группа, порядки  и
и  взаимно просты. Если $IMAGE27$ и
взаимно просты. Если $IMAGE27$ и  --- конечная неразрешимая группа, то $IMAGE29$, $IMAGE30$, $IMAGE31$ и $IMAGE32$ --- простое число $IMAGE33$ или $IMAGE34$ для некоторого простого $IMAGE35$.
--- конечная неразрешимая группа, то $IMAGE29$, $IMAGE30$, $IMAGE31$ и $IMAGE32$ --- простое число $IMAGE33$ или $IMAGE34$ для некоторого простого $IMAGE35$.
Теорема. Пусть  --- группа Шмидта;
--- группа Шмидта;  --- $IMAGE38$-разложимая группа, где $IMAGE39$. Если $IMAGE40$ и
--- $IMAGE38$-разложимая группа, где $IMAGE39$. Если $IMAGE40$ и  --- простая группа, то $IMAGE42$, $IMAGE30$ или $IMAGE31$ и $IMAGE32$ --- простое число.
--- простая группа, то $IMAGE42$, $IMAGE30$ или $IMAGE31$ и $IMAGE32$ --- простое число.
В пятом пункте доказываются следующие теоремы:
Теорема. Пусть конечная группа  является произведением своих подгрупп
является произведением своих подгрупп  и
и  взаимно простых порядков, и пусть
взаимно простых порядков, и пусть  --- бипримарная группа, а
--- бипримарная группа, а  --- 2-разложимая группа четного порядка. Предположим, что в
--- 2-разложимая группа четного порядка. Предположим, что в  есть неединичная циклическая силовская подгруппа $IMAGE52$. Тогда, если
есть неединичная циклическая силовская подгруппа $IMAGE52$. Тогда, если  неразрешима, то $IMAGE54$ изоморфна $IMAGE55$ или $IMAGE33$.
неразрешима, то $IMAGE54$ изоморфна $IMAGE55$ или $IMAGE33$.
Теорема. Пусть неразрешимая группа  является произведением бипримарной подгруппы
является произведением бипримарной подгруппы  и примарной подгруппы
и примарной подгруппы  . Тогда, если среди силовских подгрупп группы
. Тогда, если среди силовских подгрупп группы  есть циклическая, то $IMAGE54$ изоморфна одной из следующих групп:
есть циклическая, то $IMAGE54$ изоморфна одной из следующих групп:
1) $IMAGE62$;
2) $IMAGE63$;
3) $IMAGE64$;
4) $IMAGE65$;
5) $IMAGE66$;
6) $IMAGE67$, где $IMAGE68$ --- силовская 3-подгруппа;
7) $IMAGE69$, порядок  равен $IMAGE71$, а $IMAGE72$.
равен $IMAGE71$, а $IMAGE72$.
1. Основные обозначения
|  | группа |
| $IMAGE74$ | $IMAGE75$ является подгруппой группы  |
| $IMAGE77$ | $IMAGE75$ является нормальной подгруппой группы  |
| $IMAGE80$ | прямое произведение подгрупп  и и  |
| $IMAGE83$ | подгруппа Фраттини группы  |
| $IMAGE85$ | фактор-группа группы  по $IMAGE87$ по $IMAGE87$ |
| $IMAGE88$ | множество всех простых делителей натурального числа $IMAGE35$ |
| $IMAGE90$ | множество всех простых делителей порядка группы  |
| $IMAGE92$ | коммутант группы  |
| $IMAGE94$ | индекс подгруппы $IMAGE75$ в группе  |
2. Разрешимость факторизуемой группы с разложимыми факторами
Конечная группа называется $IMAGE7$-разложимой для простого числа $IMAGE7$, если силовская $IMAGE7$-подгруппа выделяется в ней прямым множителем. Нильпотентная группа $IMAGE7$-разложима для каждого $IMAGE7$. Через $IMAGE102$ обозначается множество всех простых делителей порядка группы $IMAGE103$.
Теорема Пусть  и
и  --- подгруппы конечной группы
--- подгруппы конечной группы  и пусть
и пусть 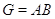 . Если подгруппы
. Если подгруппы  и
и  $IMAGE7$-разложимы для каждого $IMAGE8$, то
$IMAGE7$-разложимы для каждого $IMAGE8$, то  разрешима.
разрешима.
Теорема (1) обобщает известную теорему Виландта-Кегеля о разрешимости конечной группы, являющейся произведением нильпотентных подгрупп [??].
Для доказательства теоремы (2) нам потребуется следующая лемма(3), которая несколько уточняет лемму Кегеля(4). Напомним, что $IMAGE113$ --- центр $IMAGE103$, а если $IMAGE115$ --- подгруппа группы $IMAGE103$, то $IMAGE117$ --- наименьшая нормальная в $IMAGE103$ подгруппа, содержащая $IMAGE115$. Группа $IMAGE103$ называется $IMAGE7$-замкнутой, если в ней силовская $IMAGE7$-подгруппа $IMAGE123$ нормальна.
Лемма Пусть  и
и  --- подгруппы конечной группы
--- подгруппы конечной группы  , обладающие следующими свойствами:
, обладающие следующими свойствами:
1) $IMAGE127$ для всех $IMAGE128$;
2) $IMAGE129$, где $IMAGE130$.
Тогда $IMAGE131$.
Доказательство. Воспользуемся методом доказательства леммы Кегеля. Пусть $IMAGE132$ --- наибольшая $IMAGE38$-подгруппа, содержащая  и перестановочная с каждой подгруппой, сопряженной с
и перестановочная с каждой подгруппой, сопряженной с  . Предположим, что $IMAGE136$ не содержится в $IMAGE137$. Это означает, что существуют элементы $IMAGE128$ и $IMAGE139$ такие, что $IMAGE140$ не принадлежит $IMAGE137$. Поэтому $IMAGE132$ --- собственная подгруппа в $IMAGE143$ и $IMAGE144$ есть $IMAGE38$-группа. Кроме того, $IMAGE146$ перестановочна с каждой сопряженной с
. Предположим, что $IMAGE136$ не содержится в $IMAGE137$. Это означает, что существуют элементы $IMAGE128$ и $IMAGE139$ такие, что $IMAGE140$ не принадлежит $IMAGE137$. Поэтому $IMAGE132$ --- собственная подгруппа в $IMAGE143$ и $IMAGE144$ есть $IMAGE38$-группа. Кроме того, $IMAGE146$ перестановочна с каждой сопряженной с  подгруппой, так как этим свойством обладает $IMAGE132$. Теперь $IMAGE149$ для всех $IMAGE128$, что противоречит выбору $IMAGE132$.
подгруппой, так как этим свойством обладает $IMAGE132$. Теперь $IMAGE149$ для всех $IMAGE128$, что противоречит выбору $IMAGE132$.
Итак, $IMAGE152$. Значит, $IMAGE153$ и $IMAGE154$ --- нормальная в $IMAGE155$ $IMAGE38$-подгруппа. Из условия 2) следует, что $IMAGE157$ и $IMAGE158$. Так как $IMAGE159$ и $IMAGE160$, то $IMAGE161$. Поэтому $IMAGE131$.
Лемма Пусть конечная группа 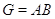 с $IMAGE7$-замкнутыми подгруппами
с $IMAGE7$-замкнутыми подгруппами  и
и  . Если $IMAGE167$, то $IMAGE168$.
. Если $IMAGE167$, то $IMAGE168$.
Доказательство. Так как $IMAGE169$, то $IMAGE170$ для всех $IMAGE171$, $IMAGE172$. Первое условие леммы (5) выполнено. Так как выполняется и второе, то $IMAGE168$.
Секцией группы $IMAGE103$ называется фактор-группа некоторой подгруппы из $IMAGE103$. Если $IMAGE103$ не содержит секций, изоморфных симметрической группе $IMAGE177$ четырех символов, то $IMAGE103$ называется $IMAGE177$-свободной.
Лемма Если конечная группа  не является $IMAGE177$-свободной, то существуют $IMAGE182$-подгруппы $IMAGE75$ и $IMAGE184$ такие, что $IMAGE184$ нормальна в $IMAGE75$ и $IMAGE187$.
не является $IMAGE177$-свободной, то существуют $IMAGE182$-подгруппы $IMAGE75$ и $IMAGE184$ такие, что $IMAGE184$ нормальна в $IMAGE75$ и $IMAGE187$.
Доказательство. По условию в группе  существует секция $IMAGE189$, изоморфная $IMAGE177$. Пусть $IMAGE191$ --- нормальная в
существует секция $IMAGE189$, изоморфная $IMAGE177$. Пусть $IMAGE191$ --- нормальная в  подгруппа индекса $IMAGE193$, содержащая подгруппу
подгруппа индекса $IMAGE193$, содержащая подгруппу  с индексом $IMAGE195$. По лемме Фраттини $IMAGE196$, где $IMAGE197$ --- силовская $IMAGE20$-подгруппа из
с индексом $IMAGE195$. По лемме Фраттини $IMAGE196$, где $IMAGE197$ --- силовская $IMAGE20$-подгруппа из  , Так как $IMAGE197$ имеет индекс $IMAGE20$ в силовской $IMAGE20$-подгруппе из
, Так как $IMAGE197$ имеет индекс $IMAGE20$ в силовской $IMAGE20$-подгруппе из  , то $IMAGE204$ разрешима и содержит $IMAGE182$-холловскую подгруппу $IMAGE75$. Кроме того, $IMAGE207$ и $IMAGE208$.
, то $IMAGE204$ разрешима и содержит $IMAGE182$-холловскую подгруппу $IMAGE75$. Кроме того, $IMAGE207$ и $IMAGE208$.
Лемма Конечная группа, содержащая нильпотентную $IMAGE182$-холловскую подгруппу, $IMAGE21$-разрешима.
Доказательство. Достаточно показать непростоту группы  в случае, когда $IMAGE21$ делит $IMAGE213$. Предположим, что
в случае, когда $IMAGE21$ делит $IMAGE213$. Предположим, что  простая и $IMAGE21$ делит $IMAGE213$. В $IMAGE177$-свободных группах нет нильпотентных $IMAGE182$-холловских подгрупп [??], отличных от $IMAGE20$-силовской. Если
простая и $IMAGE21$ делит $IMAGE213$. В $IMAGE177$-свободных группах нет нильпотентных $IMAGE182$-холловских подгрупп [??], отличных от $IMAGE20$-силовской. Если  не $IMAGE177$-свободна, то по лемме (??) существует ненильпотентная $IMAGE182$-подгруппа. Это противоречит теореме Виландта [??]. Лемма доказана.
не $IMAGE177$-свободна, то по лемме (??) существует ненильпотентная $IMAGE182$-подгруппа. Это противоречит теореме Виландта [??]. Лемма доказана.
Через $IMAGE223$ обозначим произведение всех разрешимых нормальных в  подгрупп.
подгрупп.
Лемма Пусть конечная группа 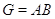 и пусть
и пусть  разрешима, а $IMAGE227$ взаимно прост с $IMAGE193$. Если в
разрешима, а $IMAGE227$ взаимно прост с $IMAGE193$. Если в  существует нилъпотентная $IMAGE182$-холловская подгруппа, то
существует нилъпотентная $IMAGE182$-холловская подгруппа, то  разрешима.
разрешима.
Доказательство. Если  --- $IMAGE233$-группа, то
--- $IMAGE233$-группа, то  разрешима по лемме Сыскина(2). Пусть $IMAGE21$ делит $IMAGE213$ и $IMAGE87$ --- минимальная нормальная в
разрешима по лемме Сыскина(2). Пусть $IMAGE21$ делит $IMAGE213$ и $IMAGE87$ --- минимальная нормальная в  подгруппа. Если $IMAGE239$, то $IMAGE240$ и $IMAGE241$ разрешима по индукции, поэтому разрешима и $IMAGE87$. Пусть $IMAGE243$. Тогда $IMAGE244$ и $IMAGE85$ имеет порядок взаимно простой с $IMAGE193$. Значит нильпотентная $IMAGE182$-холловская подгруппа из
подгруппа. Если $IMAGE239$, то $IMAGE240$ и $IMAGE241$ разрешима по индукции, поэтому разрешима и $IMAGE87$. Пусть $IMAGE243$. Тогда $IMAGE244$ и $IMAGE85$ имеет порядок взаимно простой с $IMAGE193$. Значит нильпотентная $IMAGE182$-холловская подгруппа из  содержится в $IMAGE87$ и $IMAGE87$ $IMAGE21$-разрешима по лемме(2). Из минимальности $IMAGE87$ следует, что $IMAGE87$ разрешима. Итак, в любом случае
содержится в $IMAGE87$ и $IMAGE87$ $IMAGE21$-разрешима по лемме(2). Из минимальности $IMAGE87$ следует, что $IMAGE87$ разрешима. Итак, в любом случае  содержит разрешимую нормальную подгруппу $IMAGE87$. Фактор-группа $IMAGE85$ удовлетворяет условиям леммы и по индукции разрешима. Поэтому разрешима и
содержит разрешимую нормальную подгруппу $IMAGE87$. Фактор-группа $IMAGE85$ удовлетворяет условиям леммы и по индукции разрешима. Поэтому разрешима и  . Лемма доказана.
. Лемма доказана.
Теорема (??) вытекает из следующей более общей теоремы
Теорема Пусть  и
и  --- подгруппы конечной группы
--- подгруппы конечной группы  и пусть
и пусть 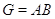 . Предположим, что
. Предположим, что  и
и  --- $IMAGE7$-замкнуты для каждого $IMAGE17$. Если
--- $IMAGE7$-замкнуты для каждого $IMAGE17$. Если  и
и  $IMAGE20$-разложимы и $IMAGE21$-разложимы, то
$IMAGE20$-разложимы и $IMAGE21$-разложимы, то  разрешима.
разрешима.
Доказательство индукцией по порядку  . Пусть $IMAGE87$ --- минимальная нормальная в
. Пусть $IMAGE87$ --- минимальная нормальная в  подгруппа. Фактор-группа $IMAGE274$, а подгруппы $IMAGE275$ и $IMAGE276$ будут $IMAGE20$- и $IMAGE21$-разложимыми и $IMAGE7$-замкнутыми для каждого $IMAGE280$. По индукции $IMAGE85$ разрешима, а $IMAGE87$ неразрешима. Поэтому $IMAGE283$ и $IMAGE284$. Следовательно, в
подгруппа. Фактор-группа $IMAGE274$, а подгруппы $IMAGE275$ и $IMAGE276$ будут $IMAGE20$- и $IMAGE21$-разложимыми и $IMAGE7$-замкнутыми для каждого $IMAGE280$. По индукции $IMAGE85$ разрешима, а $IMAGE87$ неразрешима. Поэтому $IMAGE283$ и $IMAGE284$. Следовательно, в  единственная минимальная нормальная подгруппа.
единственная минимальная нормальная подгруппа.
Пусть $IMAGE17$ и пусть $IMAGE287$ и $IMAGE288$ --- силовские $IMAGE7$-подгруппы из  и
и  соответственно. Так как
соответственно. Так как  и
и  р-замкнуты и $IMAGE283$, то $IMAGE168$ по лемме (??). Но
р-замкнуты и $IMAGE283$, то $IMAGE168$ по лемме (??). Но  содержит точно одну минимальную нормальную подгруппу. Поэтому либо $IMAGE297$, либо $IMAGE298$. Итак для каждого $IMAGE7$, либо $IMAGE7$ не делит $IMAGE301$, либо $IMAGE7$ не делит $IMAGE227$. Следовательно, порядки
содержит точно одну минимальную нормальную подгруппу. Поэтому либо $IMAGE297$, либо $IMAGE298$. Итак для каждого $IMAGE7$, либо $IMAGE7$ не делит $IMAGE301$, либо $IMAGE7$ не делит $IMAGE227$. Следовательно, порядки  и
и  взаимно просты. Но теперь $IMAGE306$ --- простая группа.
взаимно просты. Но теперь $IMAGE306$ --- простая группа.
Так как группа Судзуки $IMAGE307$ нефакторизуема(4), то по теореме Глаубермана (4)порядок  делится на $IMAGE21$, а по теореме Фомина (2) порядок одного из факторов, пусть порядок
делится на $IMAGE21$, а по теореме Фомина (2) порядок одного из факторов, пусть порядок  , делится на $IMAGE193$. Теперь в
, делится на $IMAGE193$. Теперь в  существует нильпотентная $IMAGE182$-холловская подгруппа. По лемме (3)группа
существует нильпотентная $IMAGE182$-холловская подгруппа. По лемме (3)группа  разрешима. Теорема доказана.
разрешима. Теорема доказана.
3. О произведении 2-разложимой группы и группы Шмидта Пусть конечная группа  является произведением двух своих подгрупп
является произведением двух своих подгрупп  и
и  , причем
, причем  есть группа Шмидта, т. е. ненильпотентная группа, все собственные подгруппы которой нильпотентны. Признаки разрешимости группы
есть группа Шмидта, т. е. ненильпотентная группа, все собственные подгруппы которой нильпотентны. Признаки разрешимости группы  при дополнительных ограничениях на подгруппы
при дополнительных ограничениях на подгруппы  и
и  получили Б. Хупперт(2), В. А. Ведерников(4), И. П. Докторов(4), П. И. Трофимов(3). Если
получили Б. Хупперт(2), В. А. Ведерников(4), И. П. Докторов(4), П. И. Трофимов(3). Если  дедекиндова, т. е. в
дедекиндова, т. е. в  все подгруппы инвариантны, то простая группа
все подгруппы инвариантны, то простая группа  описана автором в(5). Как сообщил недавно С. А. Сыскин, им изучена простая группа
описана автором в(5). Как сообщил недавно С. А. Сыскин, им изучена простая группа  в случае, когда
в случае, когда  --- нильпотентная группа.
--- нильпотентная группа.
Основным результатом настоящей заметки является
Теорема Пусть  есть группа Шмидта,
есть группа Шмидта,  --- 2-разложимая группа, порядки
--- 2-разложимая группа, порядки  и
и  взаимно просты. Если $IMAGE27$ и
взаимно просты. Если $IMAGE27$ и  --- конечная неразрешимая группа, то $IMAGE29$, $IMAGE30$, $IMAGE31$ и $IMAGE32$ --- простое число $IMAGE33$ или $IMAGE34$ для некоторого простого $IMAGE35$.
--- конечная неразрешимая группа, то $IMAGE29$, $IMAGE30$, $IMAGE31$ и $IMAGE32$ --- простое число $IMAGE33$ или $IMAGE34$ для некоторого простого $IMAGE35$.
$IMAGE340$ обозначает наибольшую разрешимую инвариантную в 