Курсова робота
АРИФМЕТИЧНІ ЗАСТОСУВАННЯ ТЕОРІЇ КОНГРУЕНЦІЙ
Зміст
Вступ
1. Конгруенції та їх основні властивості
2. Ознаки подільності
3. Перевірка арифметичних дій
4. Визначення члена цифр періоду при перетворенні звичайного дробу в десятковий
5. Індекси. Загальні властивості
Висновки
Вступ Важливе місце в курсі теорії чисел посідають конгруенції та, зокрема, застосування конгруенцій. Цим питанням займалися такі видатні вчені як, Ейлер, Ферма, Б. Паскаль.
П'єр Ферма (1601-1665) - відомий свого часу юрист і радник судового парламенту в Тулузі - інтенсивно і з великим успіхом займався різними математичними питаннями. П. Ферма є одним з творців диференціального числення і теорії ймовірності, але особливо велике значення мають його роботи по теорії чисел. Більшість теоретико-числових результатів П. Ферма записувалися ним на полях екземпляра твору Діофанта „Арифметика”; Ферма зазвичай не записував доведення, а давав тільки короткі вказівки про метод, який він застосовував для отримання свого результату. Твір Ферма під назвою „Opera Varia" були видані вперше в 1679 р.
Теорема Ферма, викладена в цій главі, була висловлена в одному з листів, посланому їм в 1640 р. Френіклу. У цьому листі Ферма пише, що він отримав доведення цієї теореми; проте саме доведення не було ним опубліковане.
Перше з відомих доведень теореми Ферма належить Лейбніцу (1646-1716). Доведення Лейбніца було засноване на розгляді порівняння:
.
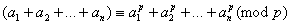Ейлер дав декілька різних доведень теореми Ферма, з яких перше відноситься до 1736 р. У 1760 р. Ейлер узагальнив теорему, надавши їй вигляду теореми 120, що носить його ім'я. Треба при цьому мати на увазі, що термінологія і позначення у Ферма і у Ейлера абсолютно відмінні від сучасних.
Блез Паскаль (1623-1662) - видатний французький математик, фізик і філософ. Математичні інтереси Паскаля дуже різноманітні: він зробив істотний внесок у розвиток аналізу нескінченно малих; разом з Ферма Паскаль є основоположником теорії ймовірностей; йому належать загальна ознака подільності будь-якого цілого числа на будь-яке інше ціле число, яка ґрунтується на знанні суми цифр числа, а також спосіб обчислення біноміальних коефіцієнтів ("Арифметичний трикутник ″); він вперше точно визначив і застосував для доведення метод повної математичної індукції
Дана курсова робота складається з 5 параграфів:
1. Конгруенції та їх основні властивості: вводяться означення конгруенції, основні властивості, основні теоремами в теорії конгруенцій - Ейлера і Ферма.
2. Ознаки подільності. В цьому параграфі розглядаються основні ознаки подільності цілих чисел, при використанні конгруенцій; метод Паскаля - загальна ознака подільності будь-якого цілого числа на будь-яке інше ціле число.
3. Перевірка арифметичних дій. В даному параграфі наведено два способи перевірки арифметичних дій: "перевірки за допомогою дев'ятки", " перевірки за допомогою одинадцяти".
4. Визначення члена цифр періоду при перетворенні звичайного дробу в десятковий. Використовуючи конгруенції можна перетворити десятковий дріб у звичайний і визначити період даного дробу.
5. Індекси. В цьому параграфі розглядають основні властивості індексів, їх загальна характеристика. Індекси по простому і складеному модулю розглядаються в окремих підпунктах.
Кожен параграф проілюстровано прикладами.
1. Конгруенції та їх основні властивості Припустимо, що т є натуральне число; розглядатимемо цілі числа у зв'язку з остачами від ділення їх на це натуральне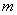 
яке називають модулем. Згідно з теоремою про ділення з остачею кожному числу а відповідатиме певна остача і від ділення а на т:
, 
.
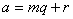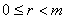Якщо двом цілим числам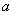 
і $IMAGE6$ відповідає одна й та сама остача $IMAGE7$ від ділення їх на т, то вони називаються конгруентними (або порівнянними) за модулем т. Це позначається символом:
$IMAGE8$ (1)
читається: а конгруентне з $IMAGE6$ за модулем т.
Деякі автори позначають це коротше:
$IMAGE10$ (1')
Співвідношення (1) [або (1')] між числами називають конгруенцією, або порівнянням.
Приклади. $IMAGE11$; $IMAGE12$; $IMAGE13$.
Теорема 1. Конгруентність чисел 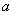і $IMAGE6$ за модулем 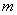рівнозначна:
а) можливості подати а у формі $IMAGE17$, де $IMAGE18$ - ціле;
б) подільності 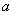- $IMAGE6$ на .
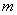Властивості:
1. Для конгруенції справджуються закони: рефлективності, симетричності і транзитивності, тобто відповідно:
a) $IMAGE22$;
б) з конгруенції $IMAGE8$ випливає, що $IMAGE24$;
в) якщо $IMAGE8$ і $IMAGE26$, то $IMAGE27$.
2. Конгруенції за одним і тим самим модулем можна почленно додавати (або віднімати).
Висновок 1. Доданок, що стоїть у якій-небудь частині конгруенції, можна переносити в іншу частину, змінивши знак на протилежний.
Висновок 2. Можна додати до обох частин або відняти від обох частин конгруенції одне й те саме число.
Висновок 3. До кожної частини конгруенції можна додати (або відняти від неї) довільне число, кратне модулю.
3. Конгруенції за одним і тим самим модулем можна почленно перемножати.
Висновок 1. Обидві частини конгруенції можна помножити на одне й те саме ціле число.
Висновок 2. Обидві частини конгруенції можна підносити до одного й того самого цілого невід'ємного степеня, тобто якщо. $IMAGE8$, то $IMAGE29$, де $IMAGE30$ - ціле $IMAGE31$.
4. Обидві частини конгруенції можна поділити на їхній спільний дільник, якщо він взаємно простий з модулем.
5. Обидві частини конгруенції і модуль можна помножити на одне й те саме натуральне число.
6. Обидві частини конгруенції і модуль можна поділити на будь-який їхній спільний дільник.
7. Якщо конгруенція має місце за кількома модулями, то вона матиме місце і за модулем, що дорівнює їхньому найменшому спільному кратному.
теорія конгруенція ейлер ферм
8. Якщо конгруенція має місце за модулем 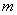, то вона матиме місце і за будь-яким дільником $IMAGE33$ цього модуля.
9. Якщо одна частина конгруенції і модуль діляться на яке-небудь ціле число, то і друга частина конгруенції ділиться на це число.
10. Числа 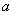і $IMAGE6$, конгруентні між собою за модулем 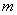, мають з ним один і той самий найбільший спільний дільник.
Візьмемо деяке натуральне число 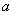, взаємно просте з модулем 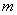, розглянемо послідовні степені 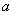: $IMAGE40$. Всі числа цієї нескінченної множини розподілені в 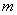класах, отже, принаймні один з цих класів повинен містити нескінченну множину степенів 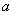. Узявши з цього класу два степені 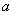і позначивши їх $IMAGE44$ і $IMAGE45$, де $IMAGE46$, матимемо $IMAGE47$. Оскільки з $IMAGE48$ слідує $IMAGE49$, то $IMAGE50$. Таким чином, для деякого $IMAGE51$маємо $IMAGE52$, причому оскільки $IMAGE53$ то $IMAGE54$. Тоді і при будь-якому натуральному $IMAGE30$ матимемо $IMAGE56$, що доводить існування нескінченної множини степенів 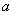, що належать класу $IMAGE58$.
П. Ферма для простого модуля, а Л. Ейлеру для будь-якого модуля вдалося вказати значення $IMAGE59$, при яких має місце рівність 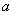$IMAGE52$. Відповідні теореми, ми їх називатимемо теоремами Ферма - Ейлера, є основою всієї теорії порівнянь і широко використовуються як в теоретичних дослідженнях, так і в арифметичних застосуваннях.
Теорема Ферма. Для будь-якого простого $IMAGE62$ і будь-якого $IMAGE63$, що не ділиться на $IMAGE62$, справедливе порівняння
$IMAGE65$.
Теорема Ейлера. Для будь-якого модуля 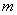і будь-якого $IMAGE63$, взаємно простого з 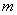, справедливе порівняння
$IMAGE69$.
2. Ознаки подільності Розрізняють загальні ознаки, що мають силу для будь-якого m і власні - для окремих значень m.
Загальну ознаку подільності виражає правило, за допомогою якого по цифрах числа N записаного в системі числення з основою g, можна судити про подільність його на інше число m.
Французький математик Блез Паскаль (1623-1662) знайшов загальну ознаку подільності. Її можна сформулювати наступним чином:
Теорема 7 (загальна ознака подільності Паскаля). Для того, щоб число N, записане в довільній g-ітій системі числення у вигляді:
$IMAGE70$,
ділилося на число m, необхідно і достатньо, щоб число $IMAGE71$ ділилося на m (де $IMAGE72$ - цифри числа N, а $IMAGE73$ - абсолютно найменші вирахування відповідних степенів $IMAGE74$ по модулю m, і = 1, 2.,n). Доведення. Нехай $IMAGE75$, де $IMAGE73$ - абсолютно найменше вирахування числа $IMAGE77$ по модулю m, (i = 1, 2., n). Тоді
$IMAGE70$ $IMAGE79$ $IMAGE80$ (1)
Число N ділиться на m тоді і тільки тоді, коли
$IMAGE70$ $IMAGE82$ (2)
З рівнянь (1) і (2) і їх транзитивності отримуємо умову, рівносильну умові (2):
$IMAGE71$ $IMAGE82$. (3)
З доведеного випливає: для того, щоб N ділилося на т, необхідно і достатньо, щоб Q ділилося на m.
Теорема доведена.
Як наслідок із загальної ознаки Паскаля витікають різні ознаки подільності. Розглянемо деякі з них (найчастіше використовувані на практиці).
Наслідок 1. Нехай m - дільник числа g - 1. Для того, щоб число, записане в g-ітій системі числення, ділилося на m, необхідно і достатньо, щоб сума його цифр ділилася на m.
Доведення. В даному випадку $IMAGE85$, а $IMAGE86$; тоді $IMAGE87$, тобто, $IMAGE88$а тому:
$IMAGE89$.
Таким чином, для того, щоб N ділилося на m, необхідно і достатньо, щоб сума цифр цього числа ділилася на m.
Для чисел, записаних в десятковій системі, з формульованої ознаки випливають відомі ознаки подільності на 9 і 3.
Наслідок 2. Нехай m - дільник числа g + I. Для того, щоб число, записане в g-ітій системі числення, ділилося на m, необхідно і достатньо, щоб різниця між сумами цифр на парних і непарних місцях ділилася на m.
Доведення. В даному випадку Звідси витікає затвердження слідства. Для чисел, записаних в десятковій системі, отримуємо $IMAGE90$ а $IMAGE91$; тоді $IMAGE92$, тобто $IMAGE93$, а тому $IMAGE94$.
Для чисел, записаних в десятковій системі, отримуємо відому ознаку подільності на 11: для того, щоб число ділилося на 11, необхідно і достатньо, щоб різниця між сумами цифр на парних і непарних місцях ділилася на 11. Наприклад, число 25 697 058 не ділиться на 11, оскільки різниця (2 + 6 + 7 + 5) - (5 + 9 + 0 + 8) = 20-22 == - 2 не ділиться на 11.
Число 905 784 ділиться на 11.
Наслідок 3. Нехай m - дільник числа $IMAGE95$. Для того, щоб число, записане в g-ітій системі числення, ділилося на m, необхідно і достатньо, щоб число, записане останніми k цифрами даного числа, ділилося на m.
Доведення. В даному випадку $IMAGE96$для $IMAGE97$ до, а тому
$IMAGE98$.
Або
$IMAGE99$. (*)
З (*) витікає твердження наслідку.
Для чисел, записаних в десятковій системі, із наслідку 3 випливає цілий ряд ознак подільності.
1) Основа $IMAGE100$ (де $IMAGE101$) ділиться на 2, 5, 10.
В цьому випадку отримаємо ознаки подільності на 2, 5, 10.
а) Для подільності числа на 2 необхідно і достатньо, щоб остання цифра була парною.
б) Для подільності числа на 5 необхідно і достатньо, щоб остання цифра ділилася на 5 (остання цифра 0 або 5).
в) Для подільності числа на 10 необхідно і достатньо, щоб воно закінчувалося нулем.
2) Дільником числа $IMAGE102$ (де $IMAGE103$) є числа 4, 25, 50, 100.
Застосовуючи наслідок 3, отримуємо ознаки подільності на 4, 25, 50, 100.
Зокрема, для того, щоб число ділилося на 4, необхідно і достатньо, щоб число, записане останніми двома ( $IMAGE103$) цифрами, ділилося на 4.
3) Аналогічно можна вивести ознаки подільності на дільників числа $IMAGE105$, тобто на числа 8, 125,. Тут потрібно розглядати число, записане останніми трьома цифрами даного числа.
Теорема 8. Для того, щоб число ділилося на 7, або на 11, або на 13, необхідно і достатньо, щоб різниця між числом записаним останніми трьома цифрами, і числом, записаним цифрами, які залишилися даного числа (або навпаки), ділилася на 7, або на 11, або на 13.
Доведення. Будь-яке число N можна представити у вигляді $IMAGE106$ де $IMAGE107$ - число, записане останніми трьома цифрами числа N, а n - цифрами, які залишилися (приклад: 829 296 = 829 1000 + 296).
Запишемо N так:
$IMAGE108$;
звідси отримаємо:
$IMAGE109$,
чи $IMAGE110$
З (4) слідує висновок: для того, щоб число N ділилося на 7, або на 11, або на 13, необхідно і достатньо, щоб число n - Q (або Q - n) ділилося на 7, або на 11, або на 13.
Приклади.
1. Чи ділиться число 56 704 на одне з чисел: 7, 11, 13? Знаходимо: Q - n = 704 - 56 = 648. Але число 648 не ділиться ні на 7, ні на 11, ні на 13; отже, і дане число не ділиться ні на одне з чисел: 7, 11, 13.
2. Чи ділиться число 454 111 на 7?
454 - 111 = 343, 343 $IMAGE111$7; отже, 454 111 $IMAGE111$7.
3. Перевірка арифметичних дій Теорія порівнянь дає