Задание: провести анализ дискретного фильтра II порядка с передаточной функцией:
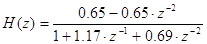
Запишем разностное уравнение:

Структура фильтра:
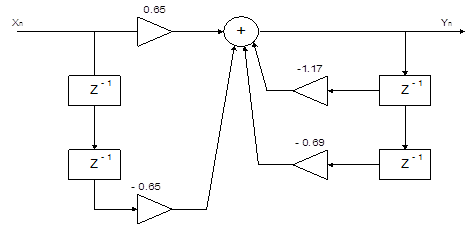
3)Рассчитаем значение нулей и полюсов:
полюса: 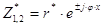
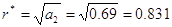
$IMAGE6$
$IMAGE7$
$IMAGE8$
нули: $IMAGE9$
$IMAGE10$
$IMAGE11$
4)Оценка устойчивости.
Все полюса передаточной функции находятся внутри единичного круга Z - плоскости $IMAGE12$. Условие $IMAGE13$ выполняется т. к. 1.17 < 1.661 < 2. Следовательно фильтр устойчив.
5)Запишем импульсную характеристику фильтра:
$IMAGE14$
$IMAGE15$
$IMAGE16$
6) Рассчитаем 5 отсчетов по формуле: $IMAGE14$, результаты занесём в таблицу 1.
Таблица 1
| n | 0 | 1 | 2 | 3 | 4 |
| hn | 4.438 | 1.627 | 1.602 | -2.561 | -1.193 |
7)График импульсной характеристики приведен на рисунке 1.
$IMAGE18$
Рисунок 1 – Импульсная характеристика фильтра
8) Запишем формулу частотной характеристики фильтра:
$IMAGE19$
9) Запишем формулу Амплитудно-частотной характеристики:
$IMAGE20$
10)Рассчитаем значения АЧХ на частотах: $IMAGE21$
$IMAGE22$
11) Выполним нормировку фильтра при условии, что $IMAGE23$
$IMAGE24$
12) График АЧХ нормированного фильтра на интервале частот от 0 до 0,5 приведен на рисунке 2.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.monax.ru
$IMAGE25$
Рисунок 2 – АЧХ нормированного фильтра.