Алгоритми Маркова
Зміст
Вступ. 3
1. Побудова алгоритмів з алгоритмів. 4
Висновки. 8
2. Нормальні Алгоритми Маркова. Побудова алгоритмів з алгоритмів. 9
Список літератури. 13
В 1956 році вітчизняним математиком А.А. Марковим було запропоновано нове уточнення поняття алгоритму, яке пізніше названий його ім'ям.
В цьому уточненні виділені нами 7 параметрів були визначено таким чином:
Сукупність початкових даних - слова в алфавіті S;
Сукупність можливих результатів - слова в алфавіті W;
Сукупність можливих проміжних результатів - слова в алфавіті
Р=S 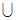 W
W 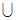 V, де V - алфавіт службових допоміжних символів.
V, де V - алфавіт службових допоміжних символів.
Дії:
Дії мають вигляд або a®g, або a a g, де a, g ÎP*, де
P* - безліч слів над алфавітом Р, і називається правилом підстановки. Значення цього правила полягає в тому, що оброблюване слово w є видимим зліва направо і шукається входження в нього слова a.
Дотепер, будуючи той або інший МТ, або НАМ ми кожного разу всі робили наново. Природно задати питання, а чи не можна при побудові, наприклад, нової МТ користуватися вже побудованою раніше МТ.
Наприклад, МТ3 з прикладу 3
U3((n) 1) =(n) 10
по суті є належним чином з'єднані МТ для U1(n) =n+1 і U2((n) 1) =(n-1) 1.
Аналогічне питання можна сформулювати для НАМ. Іншими словами чи можна акумулювати знання у формі алгоритмів так, щоб з них можна було будувати інші алгоритми.
Ми розглянемо цю проблему стосовно МТ. Проте всі сформульовані нами твердження будуть справедливі і для НАМ і для інших еквівалентних уточнень поняття алгоритму. Еквівалентність уточнень поняття алгоритму ми розглянемо пізніше.
Визначення 3.2. Говоритимемо, що МТ1 можна ефективно побудувати з МТ2 і МТ3 якщо існує алгоритм, який дозволяє, маючи програму для МТ2 і МТ3, побудувати програму для МТ3.
Визначення 3.3. Послідовною композицією МТ А і В називається така МТ З, що
область застосовності МТ А і Із співпадають;
C(a) =B(A(a)).
Іншими словами, застосування З до слова a дає такий же результат, як послідовне застосування до цього ж слова спочатку А, а потім до результату застосування А - В.
Послідовну композицію МТА і МТВ позначатимемо АoВ.
Теорема 3.1. Хай дані МТ А і В, такі, що В застосовна до результатів роботи А і QAQB= 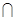 Æ.
Æ.
Тоді можна ефективно побудувати МТ З таку, що С= АoВ.
Доказ.
Як алфавіт даних і безлічі станів для МТС візьмемо об'єднання алфавітів даних і безлічі станів для А і В, тобто
DC=DADВ 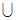 , QC= QAQB
, QC= QAQB
В програмі для А всі правила ap®b! w, де a,bÎDA* wÎ{Л, П, Н} замінимо на ap®bqoBw, де qoBÎ QB - початковий стан для В. Это забезпечить включення У в той момент, коли А свою роботу закінчила і не раніше, оскільки QAQB=Æ.
Що і т.д.
Табличний запис програми для З показана на малюнку 3.3
Рис 3.3. Структура табличного запису програм для Машини З.
Означення. Паралельною композицією Машин Тюрінга А і В назвемо таку Машину З, для якої:
DC=DADB
QC=QAQB
C(a||b) =A(a||b) °B=B(a||b) °A=A(a) ||B(b).
З цього визначення видно, що порядок застосування МТА і МТВ не впливає на результат. Він буде таким же неначебто ми незалежно застосували А до слова a, а В до слова b.
Теорема 3.2 Для будь-яких МТ А і МТ В можна ефективно побудувати МТ З таку, що С=А||В
Обгрунтовування. Ми не даватимемо тут строго доказу з причини його технічної складності. Покажемо лише обгрунтовування правильності затвердження теореми. Позначимо DC=DADB 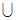 ; QC=QAQB
; QC=QAQB 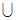 .
.
Основна проблема: як гарантувати щоб А не торкнулася слова b, а В - слово a. Для цього введемо в алфавіт DС символ ||. Додамо для всіх станів qiÎQC таких, що qiÎQA правила вигляду ||qi®||qiЛ, тобто каретка машини А буде, натикаючись на символ ||, йти вліво. Відповідно для всіх qjÎQC таких, що qjÎQB додамо правила вигляду ||qj®||qjП, тобто каретка машини В йтиме управо. Тим самим ми як би обмежуємо стрічку для А справа, а для В зліва.
Істотним тут є питання: чи не виявляться обчислювальні можливості Машини Тюрінга з напівстрічкою слабіше, ніж обчислювальні можливості Машини Тюрінга з повною стрічкою?
Виявляється справедливо наступне твердження: безліч алгоритмів, реалізовуваних МТ з напівстрічкою, еквівалентно безлічі алгоритмів, реалізовуваних МТ з повною стрічкою. Позначимо Ф(Р) Машину Тюрінга, що реалізовує алгоритм, що розпізнає:
$IMAGE8$
Теорема 3.3 Для будь-яких Машин Тюрінга А, В і Ф, мають один і той же алфавіт S, може бути ефективно побудований машина З над тим же алфавітом S, така що
$IMAGE9$
Доказ.
Позначимо: E(Р) тотожну машину, тобто Е(Р) =Р
СМІТТЮ(Р) копіюючу машину, тобто СМІТТЮ(Р) =Р||Р
де ||ÏS.
BRANCH(P) - ця машина переходить або в стан р1, або в змозі ро. Її програма складається з 4-х команд:
1qo®1р1П
||р1®||р1П
0qo®0роП
||ро®||роП
Побудуємо машину
$IMAGE10$
Ця машина будується по наступній формулі:
$IMAGE11$
Згідно теоремам 3.1 і 3.2., ми можемо побудувати машину $IMAGE12$, знаючи Е, Ф і СМІТТЮ. Тепер, маючи $IMAGE12$, BRNCH, А і В, можна побудувати машину З таким чином:
Машина $IMAGE12$ $IMAGE12$o BRANCH закінчує свою роботу або в стані р1, якщо слово P володіє потрібною властивістю, або в змозі ро, знаходячись на початку слова P. Тому, якщо прийняти у машини А стан р1, як початкове, а у машини В стан ро, як початкове, то машина А буде включений за умови, що Ф(Р) =1, а машина В буде включений, якщо Ф(Р) =0.
Правило композиції, визначуване цією теоремою записуватимемо, якщо Ф то А інакше В.
Теорема 3.4 Для будь-яких машин А і Ф можна ефективно побудувати машину L таку, що
L(P) ={ Поки Ф(Р) =1, застосовуй А }
Доказ: Замінимо в доведенні теореми 3.3 машину В машиною Е, а заключний стан в машині В замінимо на початковий стан в машині $IMAGE12$. У результаті отримаємо потрібний результат.
Теорема 3.5 (Бомм, Джакопіні, 1962)
Будь-яка Машина Тюрінга може бути побудований за допомогою операції композицій o ||, якщо Ф, то А інакше В, поки Ф застосовуй А.
Цю теорему ми даємо тут без доказу.
Слідство 3.1 Через Тезу Тюрінга, будь-яка інтуїтивно обчислювана функція може бути запрограмований в термінах цих операцій.
Слідство 3.2 Ми отримали щось подібне до мови, на якій можна описувати нову Машину Тюрінга, використовуючи описи вже існуючих, а потім, використовуючи теореми 3.1 - 3.4, побудувати її функціональну схему.
Слідство 3.3 Алгоритм - це конструктивний об'єкт. У разі Машини Тюрінга атомарними об'єктами є команди, а теорема 3.5 визначає правила композиції.
Алгоритм - конструктивний об'єкт;
Алгоритм можна будувати з інших алгоритмів;
o ||, if_then_else, while_do - універсальний набір дій по управлінню обчислювальним процесом.
Означення 3.1. Слово a називається входженням в слово w, якщо існують такі слова b і n над тим же алфавітом, що і a і w, для яких вірно: w=ban.
Якщо входження a в w знайдено, те слово a замінюється на слово g.
Всі правила постановки упорядковуються. Спочатку шукається входження для першого правила підстановки. Якщо воно знайдено, то відбувається підстановка і перетворюване слово знову є видимим зліва направо у пошуках входження. Якщо входження для першого правила не знайдено, то шукається входження для другого правила і т.д. Якщо входження знайдено для i-го правила підстановки, то відбувається підстановка, і проглядання правил починається з першого, а слово є видимим спочатку і зліва направо.
Вся сукупність правил підстановки називається схемою алгоритму.
Правило початку - проглядання правил завжди починається з першого.
Правило закінчення - виконання алгоритму закінчується, якщо:
було застосовано правило підстановки вигляду a a g,
не застосовно жодне правило підстановки з схеми алгоритму.
Правило розміщення результату - слово, отримане після закінчення виконання алгоритму.
Розглянемо приклад 1 з лекції 2:
побудувати алгоритм для обчислення
U(n) =n+1;
S={0,1,2,3,4,5,6,7,8,9}; S=W; V={*,+}.
Схема цього НАМ показана на малюнку 1.1
| $IMAGE17$ | Перегонимо службовий символ * в кінець слова n, щоб відзначити останню цифру молодших розрядів. Збільшуємо на одиницю, починаючи з цифрами молодших розрядів. | |
| $IMAGE18$ | Вводимо службовий символ * в слово, щоб їм відзначити останню цифру в слові. |
Рис.1.1 Схема НАМ для обчислення U1(n) =n+1
Неважко зміркувати, що складність цього алгоритму, виражена в кількості виконаних правил підстановки, буде рівна:
(k+1) +(l+1)
де до - кількість цифр в n, l - кількість 9, які були збільшені на 1.
Але у будь-якому випадку складність НАМ для U1(n) більше складності Машини Тюрінга для цієї ж функції, яка дорівнювала k+1.
Зверніть увагу, що у НАМ порядок проходження правил підстановки в схемі алгоритму істотно впливає на результат, тоді як для МТ він не существенен.
Побудуємо НАМ для прикладу 2 з лекції 2:
побудувати алгоритм для обчислення
U2((n) 1) =(n-1) 1
Отже, S={|}; W=S; V=Æ, тобто порожньо.
| a
Складність цього алгоритму рівна 1, тоді як складність алгоритму для Машини Тюрінга дорівнювала n.
Тепер побудуємо НАМ:
побудувати алгоритм для обчислення
U3((n) 1) =(n) 10
S={|}; W={0,1,2,3,4,5,6,7,8,9}; V=Æ
Схема цього алгоритму приведена на малюнку 3.2
1|®2
2|®3
3|®4
4|®5
5|®6
6|®7
7|®8
8|®9
9|®|0
|0®10
0|®1
|®0|
Мал.1.2 Схема НАМ для обчислення U3((n) 1) =(n) 10.
Складність цього НАМ буде n+ [log10n], що істотно менше за складність для Машини Тюрінга, що обчислює цю функцію, яка дорівнювала n2+ [log10n(log10n+1)].
Реалізацію функції U4 порівняння двох цілих чисел залишаємо читачу як вправа.
Зауваження: початкове слово треба задати у формі $IMAGE19$ * $IMAGE20$
Для нормальних алгоритмів Маркова справедлива теза, аналогічна тезі Тюрінга.
Теза Маркова: Для будь-якої інтуїтивно обчислюваної функції існує алгоритм, що її обчислює.
1. Джон Хопкрофт, Раджів Мотані, Джеффрі Ульман РОЗДІЛ 8. Введення в теорію машин Тюрінга // Введення в теорію автоматів, мов і обчислень. – М., 2002. – С528.