Вариант 6
Тема: Алгебра матриц
Задание: Выполнить действия над матрицами.
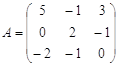
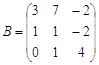
1) С=3A-(A+2B)B
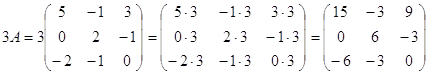
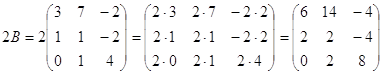
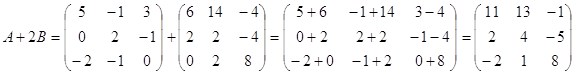
$IMAGE6$
$IMAGE7$
2) D=A2+B2+4E2
$IMAGE8$
$IMAGE9$
$IMAGE10$
$IMAGE11$
Тема: Обращение матриц
Обратить матрицу по определению:
$IMAGE12$
Определитель матрицы:
$IMAGE13$
Далее находим матрицу алгебраических дополнений (союзную матрицу):
$IMAGE14$
Обратную матрицу находим:
$IMAGE15$
По определению обратной матрицы:
$IMAGE16$
Действительно:
$IMAGE17$
Тема: решение матричных уравнений
Задание 1: Решить матричное уравнение:
$IMAGE18$
Решение.
Нахождение столбца Х сводится к умножению матрицы на обратную:
$IMAGE19$
Матрица коэффициентов А:
$IMAGE20$
Найдем обратную матрицу A-1:
Определитель матрицы A:
$IMAGE21$
Алгебраические дополнения:
$IMAGE22$ $IMAGE23$ $IMAGE24$
$IMAGE25$ $IMAGE26$ $IMAGE27$
$IMAGE28$ $IMAGE29$ $IMAGE30$
Транспонированная матрица алгебраических дополнений:
$IMAGE31$
Запишем выражение для обратной матрицы:
$IMAGE32$
Итак, выполняем умножение матриц и находим матрицу X:
$IMAGE33$
Ответ:
$IMAGE34$
Задание 2: Решить систему уравнений матричным способом
$IMAGE35$
Решение
Матричная запись уравнения:
$IMAGE36$
Матрица коэффициентов А:
$IMAGE37$
Найдем обратную матрицу A-1:
Определитель матрицы A:
$IMAGE38$
Алгебраические дополнения:
$IMAGE39$ $IMAGE40$ $IMAGE41$
$IMAGE42$ $IMAGE43$ $IMAGE44$
$IMAGE45$ $IMAGE46$ $IMAGE47$
Транспонированная матрица алгебраических дополнений (союзная матрица):
$IMAGE48$
Запишем выражение для обратной матрицы:
$IMAGE49$
Вычислим столбец неизвестных:
$IMAGE50$
Тема: Решение систем линейных уравнений методом Крамера и Гаусса
Задание 1: Исследовать и решить систему по формулам Крамера:
$IMAGE51$
Найти решение системы уравнений по методу Крамера.
Согласно методу Крамера, если определитель матрицы системы ненулевой, то система из 4-х уравнении имеет одно решение, при этом значение корней:
$IMAGE52$, $IMAGE53$, $IMAGE54$, $IMAGE55$,
Где:
$IMAGE56$ - определитель матрицы коэффициентов – ненулевой.
$IMAGE57$ - определитель матрицы полученной путем замены первого столбца матрицы коэффициентов на столбец свободных членов.
$IMAGE58$ - определитель матрицы полученной заменой второго столбца матрицы коэффициентов на столбец свободных членов.
$IMAGE59$ - определитель матрицы полученной заменой третьего столбца матрицы коэффициентов на столбец свободных членов.
$IMAGE60$ - определитель матрицы полученной заменой четвертого столбца матрицы коэффициентов на столбец свободных членов.
Итак:
$IMAGE61$
$IMAGE62$,
$IMAGE63$,
$IMAGE64$.
Задание 2: Решить эту систему по методу Гаусса.
$IMAGE51$
Метод Гаусса заключается в сведении системы к треугольному виду.
$IMAGE66$
$IMAGE67$
$IMAGE68$
$IMAGE69$
$IMAGE70$
$IMAGE71$
$IMAGE72$
Видим, что решение системы по методу Гаусса совпадает с решением по методу Крамера.