Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Самарский государственный технический университет
Кафедра: «Технология органического и нефтехимического синтеза»
КУРСОВАЯ РАБОТА
ПО КУРСУ:
«Физико-химические свойства растворов»
Выполнил: студент III – ХТ – 2 Степанов В. Н.
Принял: к. х. н., доцент Саркисова В. С.
Cамара, 2005 г.
Исходные данные:
| | Tb, К | Tc(эксп)К | Pc(эксп),bar | Vc(эксп), см3/моль | W(эксп) | Zc | yi |
| 2.3-диметилбутан | 331.13 | 499.98 | 31.27 | 358 | 0.247 | 0.270 | 0.37 |
| цис-1,2-диметилциклогексан | 402.90 | 606.00 | 29.3 | 461,73 | | | 0.22 |
| метил-третбутиловый эфир | 328.30 | 497.10 | 34.3 | 334 | | | 0.1 |
| индан | 451.10 | 684.90 | 39.5 | 389 | | | 0.31 |
Задание:
1. Для четырехкомпонентной смеси заданного состава рассчитать энтальпию, энтропию, теплоемкость в стандартном состоянии при заданной температуре.
2. Псевдокритические свойства: температуру, давление, объем, ацентрический фактор и коэффициент сжимаемости.
3. Плотность:
3.1. Ненасыщенной газовой и жидкой смеси при температуре, соответствующей приведенной температуре 0,95 в диапазоне приведенных давлений от 0,01 до 1. Построить график зависимости.
3.2. Плотность жидкой смеси на линии насыщения в диапазоне температур от 298К до критической с шагом 25К. Построить график зависимости.
4. Энтальпию, энтропию, теплоемкость смеси при заданной температуре в диапазоне приведенных давлений от 0,01 до 10. Построить график зависимости соответствующего свойства от давления.
5. Энтальпию испарения в стандартном состоянии при давлении отличном от 1 атм для диапазона температур для диапазона температур от 298К до критической с шагом 25К.
6. «Кажущуюся» стандартную энтальпию образования смеси в жидком состоянии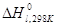 
.
7. Вязкость смеси при температуре 730 К и приведенном давлении 10.
8. Теплопроводность смеси при температуре 730К и приведенном давлении 10.
Решение:
1. Для расчета т/д характеристик смеси нужно знать параметры компонентов этой смеси.
Для 2,3-диметилбутана при вычислении 
используем следующую формулу:
где для диапазона температур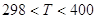 
:
и т.д.
Значения $IMAGE6$, $IMAGE7$ и $IMAGE8$ рассчитаны по табличным данным методом Бенсона.
При расчете $IMAGE9$ используем уже найденные значения $IMAGE10$ для диапазонов температур:
$IMAGE11$
$IMAGE12$
При расчете $IMAGE13$ получаем: $IMAGE14$.
Для цис-1,2-диметилциклогексана при вычислении используем следующую формулу:
$IMAGE16$где для диапазона температур $IMAGE17$:
$IMAGE18$ и т.д.
Значения $IMAGE6$, $IMAGE7$ и $IMAGE8$ рассчитаны по табличным данным методом Бенсона.
При расчете $IMAGE9$ цис-1,2-диметилциклогексана используем уже найденные значения $IMAGE10$ для диапазонов температур:
$IMAGE24$
$IMAGE25$
При расчете $IMAGE13$ цис-1,2-диметилциклогексана получаем: $IMAGE27$.
Для метил-третбутилового эфира при вычислении используем следующую формулу:
$IMAGE29$где для диапазона температур :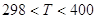
$IMAGE31$
и т.д.
Значения $IMAGE32$, $IMAGE7$ и $IMAGE8$ рассчитаны по табличным данным методом Бенсона.
При расчете $IMAGE9$ используем уже найденные значения $IMAGE10$ для диапазонов температур:
$IMAGE37$
$IMAGE38$При расчете $IMAGE13$ получаем: $IMAGE40$.
Для индана при вычислении используем следующую формулу:
$IMAGE42$где для диапазона температур :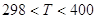
$IMAGE44$
и т.д.
Значения $IMAGE45$, $IMAGE7$ и $IMAGE8$ рассчитаны по табличным данным методом Бенсона.
При расчете $IMAGE9$ используем уже найденные значения $IMAGE10$ для диапазонов температур:
$IMAGE50$
$IMAGE51$.
При расчете $IMAGE13$ получаем: $IMAGE53$.
Для смесей в состоянии идеального газа энтальпия, энтропия и теплоемкость рассчитываются аддитивно с учетом переменной состава:
$IMAGE54$;
$IMAGE55$;
$IMAGE56$.
2. Псевдокритический объем смеси определяется, как функция от состава смеси и критических объемов чистых компонентов смеси: $IMAGE57$, при этом получена матрица:
| | 1 | 2 | 3 | 4 |
| 1 | 392.0816 | 265.4731 | 102.3749 | 342.5268 |
| 2 | 265.4731 | 178.7814 | 69.4187 | 231.5124 |
| 3 | 102.3749 | 69.4187 | 26.7200 | 89.4788 |
| 4 | 342.5268 | 231.5124 | 89.4788 | 299.0632 |
Псевдокритическая температура рассчитывается, как функция от критической температуры, критического объема и состава смеси:
$IMAGE58$
При этом получена следующая матрица:
| | 1 | 2 | 3 | 4 |
| 1 | 196032.9584 | 146127.9295 | 51037.78151 | 200440 |
| 2 | 146127.9295 | 108341.532 | 38100.82371 | 149150.3 |
| 3 | 51037.78151 | 38100.82371 | 13282.512 | 52210.23 |
| 4 | 200440.0092 | 149150.2849 | 52210.23284 | 204828.4 |
Ацентрический фактор смеси рассчитывается аддитивно: $IMAGE59$.
Ацентрические факторы чистых компонентов смеси рассчитываются по уравнению:
$IMAGE60$,
$IMAGE61$ $IMAGE62$, где: $IMAGE63$, Рс – критическое давление, атм.
Псевдокритическое давление смеси рассчитывается через уравнение: $IMAGE64$, где: $IMAGE65$ – псевдокритический коэффициент сжимаемости, определяемый с помощью таблиц Ли-Кесслера и разложения Питцера.
3.
3.1. Плотность ненасыщенной газовой и жидкой смеси определяем по формуле: $IMAGE66$, где:
$IMAGE67$- молекулярная масса смеси, определяемая по правилу аддитивности.
$IMAGE68$ - объем смеси, определяемый по уравнению Менделеева-Клапейрона:
$IMAGE69$,
$IMAGE70$ - фактор сжимаемости смеси, определяемый с помощью разложения Питцера и таблиц Ли-Кесслера.
Для диапазона приведенных давлений от 0,01 до 1 имеем:
| Pr | P, атм | z(0) | z(1) | z | Vm, см3/моль | ρm, г/см3 |
| 0.01 | 0.3316 | 0.9961 | -0.0012 | 0.9958 | 135736.7088 | 0.00075 |
| 0.05 | 1.6578 | 0.9803 | -0.0062 | 0.9787 | 26680.6560 | 0.00382 |
| 0.10 | 3.3156 | 0.96 | -0.0126 | 0.9567 | 13040.6132 | 0.00782 |
| 0.20 | 6.6312 | 0.9174 | -0.0262 | 0.9105 | 6205.5229 | 0.01644 |
| 0.40 | 13.2624 | 0.8206 | -0.0589 | 0.8051 | 2743.5055 | 0.03719 |
| 0.60 | 19.8936 | 0.6967 | -0.1110 | 0.6674 | 1516.3113 | 0.06728 |
| 0.80 | 26.5248 | 0.141 | -0.0540 | 0.1268 | 215.9884 | 0.47236 |
| 1.00 | 33.1559 | 0.1705 | -0.0607 | 0.1545 | 210.5945 | 0.48446 |
| 1.20 | 39.7871 | 0.1998 | -0.0678 | 0.1819 | 206.6516 | 0.49370 |
| 1.50 | 49.7339 | 0.2432 | -0.0788 | 0.2224 | 202.1250 | 0.50476 |