Прогнозирование  органических соединений
органических соединений
В целом использование метода Бенсона для расчета энтропий органических соединений в состоянии идеального газа аналогично подходу, рассмотренному при прогнозировании энтальпий образования. Однако имеются и существенные отличия: необходимо вводить поправки на симметрию молекул и пространственную изомерию; причиной тому служит сама природа этого свойства.
Статистическая термодинамика показывает, что энтропию газа можно рассматривать как сумму составляющих, относящихся к различным формам движения молекулы в целом и движения частиц, ее образующих. Сгруппировав их по характеру движения частиц, получим
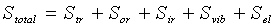 , (2.6)
, (2.6)
где 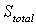 - абсолютная энтропия всей молекулы,
- абсолютная энтропия всей молекулы, 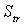 - энтропия поступательного движения молекулы,
- энтропия поступательного движения молекулы, 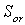 - энтропия вращательного движения молекулы, $IMAGE6$ - энтропия вращательного движения атомов и атомных групп, составляющих молекулу (энтропия внутреннего вращения), $IMAGE7$ - энтропия колебательного движения атомов и атомных групп в молекуле, $IMAGE8$ - энтропия движения электронов. Некоторые из вкладов в энтропию являются суммой более частных составляющих.
- энтропия вращательного движения молекулы, $IMAGE6$ - энтропия вращательного движения атомов и атомных групп, составляющих молекулу (энтропия внутреннего вращения), $IMAGE7$ - энтропия колебательного движения атомов и атомных групп в молекуле, $IMAGE8$ - энтропия движения электронов. Некоторые из вкладов в энтропию являются суммой более частных составляющих.
Каждая из этих форм движения материи усиливается при повышении температуры, что приводит к увеличению энтропии. Причем характер изменений вкладов в энтропию, зависящий от температуры, неодинаков для различных форм движения. Из сказанного ясно, что энтропия вещества весьма чувствительна к строению молекул. В случае органических соединений нередки ситуации, когда различие в энтропиях изомеров превосходит различие в энтропиях ближайших гомологов, и основной из причин этого оказывается статистический фактор.
Одной из статистических поправок, которые необходимо учитывать при расчете энтропии вещества методом Бенсона, является поправка к вращательной энтропии на симметрию молекул. При этом полное число симметрии молекулы $IMAGE9$ (total - общий) разбивают на два слагаемых:
* на число симметрии наружного вращения молекулы в целом - $IMAGE10$ (наружное - external) и
* число симметрии вращающейся части молекулы или число симметрии внутреннего вращения $IMAGE11$ (внутреннее - internal). Полное число симметрии ( $IMAGE9$) является произведением всех чисел симметрии молекулы:
$IMAGE13$. (2.7)
Число симметрии наружного вращения можно определить как число положений, которые может занимать жесткая многоатомная молекула (“жесткий ротатор”), совпадая при вращении со своей первоначальной конфигурацией.
Например, в двухатомных молекулах, состоящих из двух одинаковых атомов, последние могут поменяться местами при повороте молекулы на 180 градусов. Число симметрии наружного вращения таких молекул равно 2. Молекула CH4 представляет собой тетраэдр с атомами водорода в вершинах. Простым вращением молекулы вокруг каждой из связей “углерод-водород” можно получить 12 идентичных конфигураций, т.е. число симметрии наружного вращения молекулы метана равно 12.
Простой способ расчета числа симметрии для наружного вращения молекулы состоит в перемножении чисел, определяющих степень симметрии всех независимых осей, на количество этих осей. Так, для рассмотренной молекулы метана имеем четыре независимые оси третьего порядка, каждая из которых совпадает со связью С–Н. Вокруг этих осей происходит вращение молекулы. Таким образом, число симметрии наружного вращения молекулы метана равно 12 ( $IMAGE10$ = 4·3 = 12). Молекула бензола имеет шесть осей второго порядка: три из них проходят через углеродные атомы, расположенные напротив друг друга,
$IMAGE15$
а три делят пополам углерод-углеродные связи. Все оси симметрии проходят через центр симметрии молекулы бензола. Таким образом, число симметрии наружного вращения молекулы бензола равно 12 ( $IMAGE10$= 6·2 = 12).
Если часть молекулы способна вращаться относительно остальной ее части, то симметрия вращающейся части вносит дополнительные нефиксированные положения. Это приводит к необходимости введения второго числа симметрии - $IMAGE11$.
Так, полное число симметрии молекул нормальных алканов равно 18 ( $IMAGE9$ = = 2·9 = 18), где 2 - число симметрии наружного вращения молекулы по оси второго порядка, перпендикулярной основной цепи углерод-углеродных связей, а 9 - произведение чисел симметрии двух концевых метильных групп, каждая из которых имеет ось вращения третьего порядка.
Для молекул разветвленных углеводородов с количеством метильных групп, равным “n”, число симметрии внутреннего вращения составляет $IMAGE19$, а общее число симметрии будет равно $IMAGE20$ и может принимать весьма большие значения. Например, для неопентана (2,2-диметилпропана) $IMAGE21$ где 12 - число симметрии наружного вращения молекулы, 3 - ось симметрии третьего порядка в метильных группах, 4 - количество метильных групп в молекуле.
При расчете энтропии органических соединений других классов необходимо учитывать возможность заторможенного вращения прочих структурных фрагментов. Например, в молекулах ароматических углеводородов ось симметрии второго порядка имеют незамещенный фенил (C6H5 -) и пара-фенилен (-С6H4-).
Числа симметрии молекул некоторых ароматических углеводородов приведены в табл. 2.1, а для большой выборки алканов представлены в табл. 2.5.
Таблица 2.1
| Соединение | Формула | $IMAGE22$ | $IMAGE23$ | $IMAGE9$ |
| Толуол | С7H8 | 1 | 3·2 = 6 | 6 |
| Этилбензол | С8H10 | 1 | 3·2 = 6 | 6 |
| о-Ксилол | С8H10 | 2 | 32 = 9 | 18 |
| м-Ксилол | С8H10 | 2 | 32 = 9 | 18 |
| п-Ксилол | С8H10 | 2 | 2·32 = 18 | 36 |
| 1,3,5-Триметилбензол | С9H12 | 3·2 = 6 | 33 = 27 | 162 |
| Гексаметилбензол | С12H18 | 6·2 = 12 | 36 = 729 | 8748 |
| 1,1-Дихлорэтилен | С2Н2Сl2 | 1·2 = 2 | 1 | 2 |
| 2,2-Диметилпропан | С5Н12 | 4·3 = 12 | 34 = 81 | 972 |
| 1,4-Дитретбутилбензол | С14Н32 | 1·2 = 2 | 36·32·2 = 13122 | 26244 |
| 2-[3,5-бис(3-Трихлорме-тилфенил)]-Фенилбутан | С24Н20Cl6 | 1 | |