База рефератов

Академия ФСО России

Кафедра Физики

Тема:

«Законы Кирхгофа и их применение для расчета электрических цепей»

Орел-2009

Содержание

Первый закон Кирхгофа

Второй закон Кирхгофа

Расчет сложных цепей с помощью уравнений Кирхгофа

Первый закон Кирхгофа

Алгебраическая сумма токов в ветвях, сходящихся к любому узлу электрической цепи, тождественно равна нулю. Согласно этому закону, если к некоторому узлу цепи подсоединено n ветвей с токами i₁, i₂, ..., i_n, то в любой момент времени

,

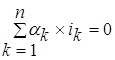где , если направление тока положительно и ориентировано от узла (ток выходит из узла), или 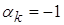, если ток входит в узел. Таким образом, любому узлу цепи соответствует уравнение, связывающее токи в ветвях цепи, соединенных с данным узлом.

В качестве примера приведем схему на рисунке 1.

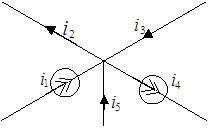
Рис.1.

В соответствии с первым законом Кирхгофа:

.

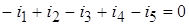Общее число уравнений, которое можно составить по первому закону Кирхгофа для цепи, равно числу узлов цепи $IMAGE6$.

Так, для четырех узлов графа (рисунок 2) можно составить следующие четыре уравнения:

$IMAGE7$
Рис.2.

узел 1: $IMAGE8$,

узел 2: $IMAGE9$,

узел 3: $IMAGE10$,

узел 4: $IMAGE11$.

Первый закон Кирхгофа часто называют законом Кирхгофа для токов и сокращенно в тексте обозначают ЗКТ.

Число независимых уравнений равно трем, так как любое из этих уравнений отличается от суммы трех остальных только знаком. Итак, если цепь содержит $IMAGE6$ узлов, то для неё можно составить по первому закону Кирхгофа $IMAGE13$ независимых уравнений. Совокупность из N узлов цепи, уравнения для которых образуют систему линейно независимых уравнений, называют совокупностью независимых узлов цепи.

Примеры на применение первого закона Кирхгофа. Параллельное соединение элементов

В качестве примера на применение первого закона Кирхгофа рассмотрим параллельное соединение нескольких элементов активных сопротивлений, конденсаторов, катушек индуктивности.

Особенностью параллельного соединения нескольких элементов является равенство напряжений, приложенных к зажимам любого из элементов, входящих в соединение. Цепь при таком соединении характеризуется только одним независимым узлом.

Пусть параллельно соединены n элементов активного сопротивления. Если выбрать направления отчетов токов в элементах такими как это показано на рисунке 3, то согласно первому закону Кирхгоффа при параллельном соединении элементов запишем:

	$IMAGE14$

u

Рис.3.

$IMAGE15$;

учитывая, что $IMAGE16$, имеем $IMAGE17$,

где $IMAGE18$.

Зависимость $IMAGE19$ не отличается от зависимости между напряжением на зажимах и током в элементе активного сопротивления с проводимостью G. Следовательно, цепь, составленная из нескольких сопротивлении, включенных параллельно, может быть заменена одним активным сопротивлением, при этом проводимость эквивалентного элемента равна сумме проводимостей элементов, входящих в соединение.

При параллельном соединении конденсаторов (рисунок 4) ток ветви можно определить по формуле: $IMAGE20$.

	$IMAGE21$

Рис.4.

Для вычисления общего тока необходимо просуммировать токи ветвей:

$IMAGE22$,

где $IMAGE23$_..

Таким образом, при параллельном соединении нескольких конденсаторов эквивалентная ёмкость равна сумме емкостей, входящих в соединение.

В случае параллельного соединения катушек индуктивностей (рисунок 5)

	$IMAGE24$

ток каждой из ветвей равен: $IMAGE25$.

Рис.5.

Уравнение для вычисления общего тока имеет вид:

$IMAGE26$.

Следовательно $IMAGE27$, то есть $IMAGE28$.

Это означает, что значение эквивалентной индуктивности будит меньше наименьшего из значений соединённых параллельно индуктивностей.

Второй закон Кирхгофа

Второй закон Кирхгофа формулируется следующим образом: алгебраическая сумма напряжений ветвей в любом контуре цепи тождественно равна нулю. Для замкнутого контура, изображённого на рисунке 6, можно записать соотношение:

$IMAGE29$.

	$IMAGE30$

Рис.6.

В соответствии со вторым законом Кирхгофа при обходе контура по часовой стрелке справедливо соотношение:

$IMAGE31$.

Изменение направления обхода эквивалентно изменению знаков напряжений на противоположные (умножению на минус единицу).

Примеры на применение второго закона Кирхгофа

Последовательное соединение элементов

	$IMAGE32$

Пусть n элементов активного сопротивления соединены последовательно (рисунок 7).

Рис.7.

В соответствии с выбранным направлением обхода по второму закону Кирхгофа получим уравнение:

$IMAGE33$.

характерной особенностью последовательного соединения является равенство токов в каждом из элементов, входящих в соединение.

При $IMAGE34$ запишем:

$IMAGE35$, то есть $IMAGE36$.

Таким образом, при последовательном соединении нескольких резисторов эквивалентное сопротивление равно сумме сопротивлений, входящих в соединение.

При последовательном соединении катушек индуктивности (рисунок 8) можно записать:

$IMAGE33$.

	$IMAGE38$

Рис.8.

Если $IMAGE39$, то $IMAGE40$,

следовательно $IMAGE41$.

Это означает, что эквивалентная индуктивность равна сумме индуктивностей, входящих в последовательное соединение.

В случае последовательного соединения конденсаторов (рисунок 9) по второму закону Кирхгофа можно записать:

	$IMAGE42$

$IMAGE33$.

Рис.9.

Заменяя $IMAGE44$ получим: $IMAGE45$.

Обратная ёмкость всех конденсаторов, соединенных последовательно, равна сумме обратных ёмкостей конденсаторов, входящих в соединение:

$IMAGE46$.

При этом эквивалентная ёмкость соединения будет меньше наименьшей ёмкости конденсатора, входящего в последовательное соединение.

Расчет сложных цепей с помощью уравнений Кирхгофа

Пример 1

Далеко не во всех случаях цепь представляет собой совокупность лишь последовательно и параллельно соединенных ветвей. В качестве примера рассмотрим вариант расчета с помощью уравнений Кирхгофа электрической цепи (рисунок 10). Цепь содержит $IMAGE47$ = 4 узлов и $IMAGE48$= 6 ветвей, включая источники напряжения.

$IMAGE49$

Рис.10.

Для определения всех токов и напряжений в схеме достаточно найти значения токов во всех ветвях цепи. Зная ток, проходящий через любую из ветвей цепи, можно найти как напряжение этой ветви, так и напряжение между любой парой узлов цепи.

Если мы зададимся произвольно положительными направлениями токов в ветвях цепи и пронумеруем произвольно эти токи, то по первому закону Кирхгофа можно составить $IMAGE50$ уравнений относительно токов в ветвях цепи.

По второму закону Кирхгофа будет $IMAGE51$ линейно-независимых уравнений для напряжений $IMAGE52$ ветвей схемы.

Совокупность из $IMAGE50$ уравнений по первому закону Кирхгофа, и $IMAGE51$ уравнений, составленных по второму закону Кирхгофа, образует систему $IMAGE55$ линейно – независимых уравнений. Эта система будет неоднородной системой уравнений, так как ее свободными членами являются заданные напряжения источников.

Подобная система уравнений имеет единственное решение, позволяющее найти токи в ветвях цепи, а по ним и значения напряжений между любой парой узлов цепи.

Для примера составим систему уравнений по первому закону Кирхгофа (рисунок 10).

Число уравнений: $IMAGE56$.

Узел 1: $IMAGE8$,

узел 2: $IMAGE58$,

узел 3:   $IMAGE59$.

В тоже время по второму закону Кирхгофа для контуров I, II, III можно составить систему из $IMAGE60$ уравнений.

$IMAGE61$.

Контур I:   $IMAGE62$,

контур II:   $IMAGE63$,

контур III:   $IMAGE64$.

Таким образом, решая систему из 6 уравнений с шестью неизвестными токами, например по методу Крамера, определим неизвестные. Если в цепи будет источник тока, то в системе уравнений неизвестным будет напряжение на зажимах этого источника, а ток через источник будет равен току задающего источника. Общее число неизвестных сохранится прежним.

Пример 2

Для цепи (рисунок 11) определить токи $IMAGE65$ и $IMAGE66$, если E = 20 В, I₀ = 2 A, R₁ = 15 Ом, R₂ = 85 Ом.

	$IMAGE67$

Рис.11.

Решение

Выберем направления токов $IMAGE65$, $IMAGE66$ и обхода в контуре, составим уравнения по законам Кирхгофа. Число уравнений, составляемых по первому закону Кирхгофа:

$IMAGE70$.

Число уравнений по второму закону Кирхгофа:

$IMAGE71$.

Уравнение токов для узла 1:

$IMAGE72$.                                                 (a)

Уравнение по второму закону Кирхгофа:

$IMAGE73$.                                                   (б)

Подставим в уравнения (а) и (б) числовые значения получим:

$IMAGE74$,

$IMAGE75$.

Решив эту систему, определим токи $IMAGE65$ и $IMAGE66$:

$IMAGE78$; $IMAGE79$.

Литература

1. Белецкий А.Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986.

2. Бакалов В.П. и др. Теория электрических цепей. – М.: Радио и связь, 1998.

3. Качанов Н. С. и др. Линейные радиотехнические устройства. М.: Воен. издат., 1974.

4. В.П. Попов Основы теории цепей – М.: Высшая школа, 2000