Содержание
Введение
1. Постановка задачи в рамках уравнений динамики жидкости
2. Математическая модель взаимодействия пузырьков
3. Методика решения
4. Исследование взаимодействия двух радиально пульсирующих пузырьков газа в жидкости
5. Заключение
6. Литература
7. Приложение. (Программа расчета).
Введение
К настоящему времени довольно хорошо изучена динамика отдельного пузырька газа в жидкости. Полученные в этом отношении результаты имеют важное теоретическое и прикладное значение. Вместе с тем, в реальных жидкостях, как правило, присутствует не один, а множество пузырьков, так что свойства жидкостей существенно зависят от особенностей взаимодействия между пузырьками. В силу большей сложности этот вопрос является менее изученным, хотя он и имеет важное прикладное значение.
В данной курсовой работе исследуется взаимодействия двух радиально пульсирующих пузырьков газа в жидкости ранние выведенной математической модели. В принципе, такое взаимодействие можно изучать и на основе широко известных уравнений Навье-Стокса методом прямого численного моделирования. Однако такой подход пока не используется в силу больших потребностей компьютерного времени даже на современных компьютерах с высоким быстродействием. В модели, использующейся в курсовой работе, жидкость считается невязкой несжимаемой, пузырьки – осесимметричными. Пузырьки расположены сносно. Их общая ось симметрии направлена вертикально вдоль действия силы тяжести. Пузырьки совершают нелинейные радиальные колебания, а скорости их вертикального пространственного перемещения считаются малыми. Используются три системы отсчета, одна неподвижная и две подвижные. В качестве неподвижной системы приняты декартовые координаты, а в качестве подвижных систем – сферические координаты. Начало отсчета радиальных координат в подвижных сферических системах отсчета связано с центрами пузырьков. Поверхности каждого из пузырьков представляются в виде ряда по поверхностным сферическим гармоникам нулевой, второй, третьей, четвертой и т.д. степеней. При этом сферическая гармоника нулевой степени описывает радиальную составляющую поверхности пузырька, а гармоники второй, третьей и т.д. степеней – отклонения от сферической формы в виде соответствующей гармоники (второй степени – эллипсоидальные отклонения, третьей – грушеобразные и т.д.).
Созданная математическая модель представляет собой систему обыкновенных дифференциальных уравнений второго порядка относительно радиусов пузырьков, пространственного положения их центров и амплитуды отклонений от сферической формы пузырьков в виде сферических поверхностных гармоник. При выводе этих уравнений используются частные решения уравнения Лапласа в сферической системе координат и интеграл Коши-Лагранжа.
Постановка задачи в рамках уравнений динамики жидкости
Рассматривается динамика двух газовых пузырьков в неограниченном объеме невязкой несжимаемой жидкости. Динамика жидкости описывается уравнениями
, 
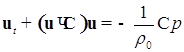. (1)
Здесь 
– время эйлеровых (неподвижных) систем координат 
, 
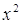, $IMAGE6$ (нижний индекс означает частную производную), $IMAGE8$– вектор скорости, $IMAGE9$– плотность жидкости, $IMAGE10$– давление, $IMAGE11$, $IMAGE12$, $IMAGE13$, $IMAGE14$–направляющие векторы пространственных координат. Здесь и далее, если не оговорено противное, по повторяющимся индексам предполагается суммирование (здесь от 1 до 3).
$IMAGE15$Пузырьки расположены вдоль вертикальной оси $IMAGE16$ неподвижной декартовой системы координат $IMAGE17$ (рис.1). $IMAGE18$
На поверхности каждого пузырька выполняются следующие условия:
кинематическое
$IMAGE19$, (2)
и динамическое
$IMAGE20$. (3)
Здесь $IMAGE21$– скорость точки поверхности пузырька, $IMAGE22$– нормаль к поверхности пузырька, верхние знаки указывают на отношение к внешней (+) и внутренней (–) сторонам поверхности.
Газ в пузырьках принимается гомобарическим (с однородным распределением давления) с давлением, изменяющимся по закону (Ван-дер-Ваальса)
$IMAGE23$, (4)
где $IMAGE24$– начальное давление газа в пузырьке, $IMAGE25$– текущий и начальный объемы пузырька, $IMAGE26$– постоянная, $IMAGE27$– показатель адиабаты.
На бесконечном удалении от пузырьков давление жидкости $IMAGE28$ совершает гармонические колебания
$IMAGE29$, (5)
где $IMAGE30$– статическое давление в жидкости, $IMAGE31$, $IMAGE32$– амплитуда и частота колебаний.
Рассматриваются случай, когда форма пузырьков в интересующем промежутке времени остается относительно близкой к сферической.
Математическая модель взаимодействия пузырьков
В пятом приближении относительно $IMAGE33$ уравнения динамики двух газовых пузырьков в вязкой сжимаемой жидкости представляют собой систему, состоящую из четырех дифференциальных уравнений относительно радиусов пузырьков $IMAGE34$, координат их центров $IMAGE35$
$IMAGE36$ $IMAGE37$ $IMAGE38$ $IMAGE39$ $IMAGE40$ $IMAGE41$ $IMAGE42$;
$IMAGE43$ $IMAGE44$ $IMAGE45$ $IMAGE46$ $IMAGE47$ $IMAGE48$ $IMAGE49$;
$IMAGE50$ $IMAGE51$ $IMAGE52$ $IMAGE53$ $IMAGE54$;
$IMAGE55$ $IMAGE56$ $IMAGE57$ $IMAGE58$ $IMAGE59$ $IMAGE60$;
Методика решения
Имея четыре уравнения второго порядка относительно радиуса и положения центра пузырьков. Вводим замену, чтобы избавится от второго порядка, и запишем уравнения 1 ого порядка:
$IMAGE61$
Получаем систему 8-и уравнений 1-го порядка относительно радиуса, положения центра пузырьков, скорость изменения радиусов и положения центра пузырьков.
$IMAGE62$ $IMAGE63$ $IMAGE64$ $IMAGE65$ $IMAGE66$ $IMAGE67$ $IMAGE68$ $IMAGE69$;
$IMAGE70$( $IMAGE71$ $IMAGE64$)/ $IMAGE73$;
$IMAGE74$ $IMAGE75$/ $IMAGE73$;
$IMAGE77$ $IMAGE78$/ $IMAGE73$;
$IMAGE80$ $IMAGE81$/ $IMAGE73$;
$IMAGE83$ $IMAGE84$/ $IMAGE73$;
$IMAGE86$ $IMAGE87$/ $IMAGE73$;
$IMAGE89$
$IMAGE90$ $IMAGE91$ $IMAGE92$ $IMAGE93$ $IMAGE94$ $IMAGE95$ $IMAGE96$ $IMAGE97$;
$IMAGE98$( $IMAGE99$ $IMAGE44$)/ $IMAGE101$;
$IMAGE102$( $IMAGE93$)/ $IMAGE101$;
$IMAGE105$( $IMAGE106$)/ $IMAGE101$;
$IMAGE108$ $IMAGE109$/ $IMAGE101$;
$IMAGE111$ $IMAGE112$/ $IMAGE101$;
$IMAGE114$( $IMAGE115$)/ $IMAGE101$;
$IMAGE117$
$IMAGE118$ $IMAGE119$ $IMAGE120$ $IMAGE121$ $IMAGE122$ $IMAGE123$;
$IMAGE124$ $IMAGE119$/ $IMAGE73$;
$IMAGE127$0;
$IMAGE128$( $IMAGE129$)/ $IMAGE73$;
$IMAGE131$( $IMAGE132$)/ $IMAGE73$;
$IMAGE134$ $IMAGE135$/ $IMAGE73$;
$IMAGE137$( $IMAGE138$)/ $IMAGE73$;
$IMAGE140$
$IMAGE141$ $IMAGE142$ $IMAGE143$ $IMAGE144$ $IMAGE145$ $IMAGE146$;
$IMAGE147$ $IMAGE142$/ $IMAGE101$;
$IMAGE150$0;
$IMAGE151$( $IMAGE152$)/ $IMAGE101$;
$IMAGE154$( $IMAGE155$)/ $IMAGE101$;
$IMAGE157$ $IMAGE158$/ $IMAGE101$;
$IMAGE160$( $IMAGE161$)/ $IMAGE101$;
$IMAGE163$
Отсюда получаем данные уравнения в следующем виде:
$IMAGE164$
Решим уравнение методом последовательных приближений.
В нулевом приближении данные уравнения записываются относительно радиуса и положения центра пузырьков.
$IMAGE165$
Подставляя выражения, находим уравнения нулевого приближения:
$IMAGE166$ $IMAGE167$
В первом приближении уравнения записываются относительно радиуса, положения центра пузырьков, скорость изменения радиусов и положения центра пузырьков. Полученное первое приближение добавляем к нулевому приближению. И так находим до пятого приближения.
$IMAGE168$ $IMAGE169$
$IMAGE170$ $IMAGE171$
$IMAGE172$ $IMAGE173$
$IMAGE174$
$IMAGE175$
$IMAGE176$
Исходя из этого, можем записать следующую систему:
$IMAGE177$
Полученные дифференциальные уравнения решаются методом Дортсмана–Принса восьмой степени точности. (Программа приведена ниже).
Исследование взаимодействия двух радиально пульсирующих пузырьков газа в жидкости
Для учета влияния вязкости и сжимаемости жидкости проводим следующую модификацию математической модели. (По аналогии с работой Дойникова[?]).
1. С учетом сжимаемости жидкости получим следующие уравнения:
$IMAGE178$ $IMAGE179$ $IMAGE180$ $IMAGE181$ $IMAGE182$ $IMAGE183$ $IMAGE184$ $IMAGE185$ $IMAGE81$ $IMAGE187$ $IMAGE188$;
$IMAGE189$ $IMAGE190$ $IMAGE191$ $IMAGE192$ $IMAGE193$ $IMAGE194$ $IMAGE45$ $IMAGE196$ $IMAGE109$ $IMAGE198$ $IMAGE199$;
Решение для нулевого приближения для одного пузырька
$IMAGE200$ $IMAGE201$ $IMAGE202$ $IMAGE203$ $IMAGE204$ $IMAGE205$;
Вводим замены:
$IMAGE206$; $IMAGE207$; $IMAGE208$;;
$IMAGE209$= $IMAGE210$ = $IMAGE211$;
$IMAGE212$ - начальное давление газа в пузырьке;
$IMAGE213$; -давление газа в пузырьке.
$IMAGE214$
$IMAGE215$
А - константа Ван-дер-Ваальса;
$IMAGE216$- коэффициент поверхностного натяжения;
$IMAGE217$ - давление газа в пузырьке;
$IMAGE30$ - статическое давление в жидкости;
$IMAGE219$- Начальный радиус пузырька;
R - Радиус пузырька;
$IMAGE220$ - Центр пузырька;
u - Вектор скорости жидкости;
$IMAGE221$-давление в жидкости на большом удалении от пузырька, где
$IMAGE222$- амплитуда и частота колебаний давления. Рассматривается лишь один период колебаний ( $IMAGE223$).
$IMAGE224$
$IMAGE9$- Плотность жидкости;
$IMAGE226$- Скорость звука в жидкости;
$IMAGE227$- Кинематический коэффициент вязкости
$IMAGE228$ - расстояние между пузырьками.
$IMAGE229$ $IMAGE230$ $IMAGE231$ $IMAGE232$ $IMAGE233$ $IMAGE234$;
$IMAGE235$ $IMAGE236$ $IMAGE237$ $IMAGE238$ $IMAGE232$ $IMAGE233$ $IMAGE241$;
Обозначим слагаемые и сомножители через: $IMAGE242$, $IMAGE243$, $IMAGE244$, $IMAGE245$, $IMAGE246$:
$IMAGE247$ $IMAGE236$; $IMAGE249$ $IMAGE250$; $IMAGE251$ $IMAGE252$;
$IMAGE253$ $IMAGE254$ $IMAGE255$; $IMAGE256$ $IMAGE257$;
$IMAGE258$ $IMAGE259$ $IMAGE260$ $IMAGE261$ $IMAGE262$ $IMAGE263$;
$IMAGE264$ $IMAGE265$ $IMAGE266$ ;
Добавляем второе уравнение: $IMAGE267$ $IMAGE268$=0 =>
$IMAGE269$ $IMAGE270$;
$IMAGE271$ $IMAGE272$;
Добавляем уравнение второго пузырька
$IMAGE273$ $IMAGE274$ $IMAGE275$ $IMAGE276$ $IMAGE277$ $IMAGE278$;
$IMAGE206$; $IMAGE207$; $IMAGE208$; $IMAGE209$= $IMAGE210$ = $IMAGE211$;
$IMAGE285$ $IMAGE286$ $IMAGE287$ $IMAGE288$ $IMAGE289$ $IMAGE278$;
$IMAGE291$ $IMAGE292$ $IMAGE293$ $IMAGE294$ $IMAGE288$ $IMAGE289$ $IMAGE297$;
$IMAGE298$ $IMAGE292$; $IMAGE300$ $IMAGE301$; $IMAGE302$ $IMAGE303$;
$IMAGE304$ $IMAGE305$ $IMAGE306$; $IMAGE307$ $IMAGE308$;
$IMAGE258$ $IMAGE310$ $IMAGE311$ $IMAGE312$ $IMAGE313$ $IMAGE314$;
$IMAGE315$ $IMAGE316$ $IMAGE266$;
Добавляем второе уравнение: $IMAGE318$ $IMAGE319$=0 =>
$IMAGE320$ $IMAGE321$;
$IMAGE322$ $IMAGE323$;
Решение для первого приближения одного пузырька
$IMAGE324$ $IMAGE119$;
$IMAGE326$;
$IMAGE327$ $IMAGE328$
$IMAGE200$ $IMAGE201$ $IMAGE202$ $IMAGE203$ $IMAGE204$ $IMAGE205$ $IMAGE335$;
$IMAGE229$ $IMAGE230$ $IMAGE231$ $IMAGE232$ $IMAGE233$ $IMAGE234$;
$IMAGE235$ $IMAGE236$( $IMAGE344$ $IMAGE238$ $IMAGE232$ $IMAGE233$ $IMAGE234$ $IMAGE65$);
$IMAGE350$;
$IMAGE351$ $IMAGE352$
Добавляем уравнение второго пузырька
$IMAGE353$ $IMAGE142$;
$IMAGE355$;
$IMAGE356$ $IMAGE357$
$IMAGE285$ $IMAGE286$ $IMAGE287$ $IMAGE288$ $IMAGE289$ $IMAGE278$ $IMAGE93$;
$IMAGE291$ $IMAGE292$ $IMAGE293$ $IMAGE294$ $IMAGE288$ $IMAGE