Контрольная работа
Техника высоких напряжений
Задача 1
Условие:
Рассчитать число электронов в лавине, развивающейся в воздухе при различных атмосферных условиях (таблица 3.1) под действием однородного электрического поля с напряжённостью Е, после прохождения лавиной пути х (таблица 3.2).
Дано: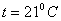 
, 
, 
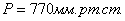кВ/см, 
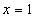см.
Найти: n=?
· Допустим, что в лавине, прошедшей расстояние х, содержится n электронов. На пути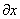 
каждый из них произведёт $IMAGE6$ ионизаций, поэтому увеличение числа электронов в лавине на пути .
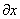$IMAGE8$ $IMAGE9$ $IMAGE10$ $IMAGE9$ $IMAGE12$
если электрическое поле однородное и напряжённость его всюду одинакова, то коэффициент свойства $IMAGE13$ не зависит от координаты х, поэтому получаем $IMAGE9$ $IMAGE15$ $IMAGE16$
Где: $IMAGE17$ эффективный коэффициент ионизации;
х – путь, пройденный лавиной.
Коэффициент $IMAGE17$ представляет собой разность между коэффициентом ударной ионизации $IMAGE13$ и коэффициентом прилипания электронов $IMAGE20$, равным числу актов захвата на пути в 1см, т.е. $IMAGE21$
· Величина $IMAGE17$ для воздуха рассчитывается по эмпирической формуле $IMAGE23$
$IMAGE24$, $IMAGE23$
$IMAGE26$ - относительная плотность воздуха
Е – напряжённость электрического поля, кВ/см.
· Относительная плотность воздуха рассчитывается:
$IMAGE27$ , $IMAGE28$
Где $IMAGE29$ и $IMAGE30$ давление и температура при нормальных атмосферных условиях: $IMAGE31$; $IMAGE32$
$IMAGE33$ и $IMAGE34$ давление и температура воздуха в расчётных условиях.
Решение:
· Рассчитываем величину $IMAGE26$ $IMAGE36$
· Рассчитываем коэффициент $IMAGE17$ при напряжённости поля кВ/см
$IMAGE39$
· Находим число электронов в лавине при 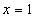см
$IMAGE41$
Задача 2
Условие:
Определить пробивное напряжение воздушного промежутка между электродами различной конфигурации при подаче на промежуток постоянного, переменного (промышленной частоты) и импульсного (стандартного) напряжений обеих полярностей.
Расстояние между электродами указано в таблице 3.3. Вид прикладываемого напряжения, форма электродов и атмосферные условия приведены в таблице 3.4.
Примечание. Разрядные напряжение, определённое по формулам, таблицам и графикам, следует привести к реальным атмосферным условиям (указанным в таблице 3.4).
Дано:
$IMAGE42$, вид прикладываемого напряжения – переменное $IMAGE43$,
Стержень-стержень, $IMAGE44$ГПа, $IMAGE45$.
Найти:
$IMAGE46$
$IMAGE47$
Промежутки стержень-стержень, являются классическим примером симметричного резконеоднородного поля. Электрическая прочность промежутка между двумя проводами очень близка к прочности промежутка стержень-стержень.
Зависимость разрядного напряжения для промежутков с резконеоднородным полем от давления имеет своеобразный характер: с ростом давления разрядные напряжения увеличиваются, в случае положительного стержня происходит снижение разрядного напряжения. Это явление можно объяснить следующим образом. При увеличении давления газа уменьшается коэффициент диффузии электронов и ионов, и положительный объёмный заряд, созданный лавиной, располагается в меньшем объёме. Поэтому напряжённость $IMAGE48$, обусловленная этим зарядом, возрастает и условие образования стримера $IMAGE49$. Соответственно снижается и разрядное напряжение.
Очевидно, что в газе под давлением следует всячески избегать использование промежутков с резконеоднородным полем.
· Из рис.1 определяем $IMAGE50$ амплитуда разрядного напряжения воздушного промежутка стержень-стержень, равного 50 см при переменном напряжении промышленной частоты и нормальных атмосферных условиях.
· Определяем разрядные напряжения для реальных условий.
$IMAGE51$
$IMAGE26$- относительная плотность воздуха.
$IMAGE53$
где $IMAGE54$- реальные давление и температура
где $IMAGE55$- давление и температура при нормальных атмосферных условиях $IMAGE56$, $IMAGE57$
$IMAGE58$
$IMAGE59$- разрядное напряжение, приведённое к реальным атмосферным условиям.
Задача 3
Условие:
Дать общую характеристику короны как одного из видов самостоятельного разряда. Объяснить природу потерь энергии на корону при переменном напряжении, существования радиопомех и акустических шумов.
Рассчитать удельные потери энергии на корону и напряжение появление короны для линии электропередачи переменного напряжения, характеризуемой следующими параметрами: номинальное напряжение линии $IMAGE60$; расщеплённые фазы расположены горизонтально и расстояние между фазами равно а.
Каждая фаза имеет n проводов радиусом $IMAGE61$ и шагом расщепления $IMAGE62$. Средняя высота подвеса проводов $IMAGE63$(таблица 3.5). Трасса ЛЭП проходит в регионе, метеорологические условия которого характеризуются продолжительностью (в часах) хорошей погоды $IMAGE64$, сухого снега $IMAGE65$, изморози $IMAGE66$, дождя и мокрого снега $IMAGE67$, относительной плотностью воздуха $IMAGE26$(таблица 3.6)
Расчёт производить согласно $IMAGE69$; $IMAGE70$
Дано: $IMAGE71$, $IMAGE72$, $IMAGE73$, $IMAGE74$, $IMAGE75$, $IMAGE76$,
$IMAGE77$, $IMAGE78$, $IMAGE79$, $IMAGE80$, $IMAGE81$
Теория:
Коронный разряд, или корона, - это самостоятельный разряд, возникающий в резконеоднородных полях, в которых ионизационные процессы могут происходить только в узкой области вблизи электродов. К такого рода полям относится и электрическое поле проводов воздушных линий электропередачи.
Начальная напряжённость коронного разряда
$IMAGE82$
которая справедлива при отрицательной полярности провода, однако может использоваться и при положительной полярности, поскольку полярности невелико.
При малых радиусов проводов $IMAGE83$ можно использовать Ф. Пика
$IMAGE84$
$IMAGE85$- коэффициент гладкости провода.
На линиях электропередачи применяются провода, витые из большого числа проволок. Витые провода не имеют гладкой поверхности, поэтому при одинаковых с гладкими проводами напряжениях и внешних диаметрах напряжённость электрического поля вблизи их поверхности бывает выше и корона возникает при меньшем напряжении. При определении начальной напряжённости коэффициент гладкости $IMAGE85$ учитывает форму поверхности витого провода. Для проводов различных марок коэффициент гладкости $IMAGE87$.
При коронном разряде в результате ионизации воздуха у поверхности провода образуется объёмный заряд того же знака, что и полярность напряжения на проводе.
Напряжённость поля у поверхности провода во время коронирования остаётся равной $IMAGE88$. Увеличение напряжения на проводе приводит к усилению ионизационных процессов, росту объёмного заряда и снижению напряжённости до $IMAGE88$. Вследствие увеличения объёмного заряда потери энергии на корону растут тем в большей степени, чем больше напряжение на проводе превосходит начальное напряжение
$IMAGE90$
$IMAGE91$- высота одиночного провода над землёй.
Так как объёмный заряд при любой полярности провода перемещается от провода к земле, напряжённость поля у поверхности провода стремится увеличиться. Однако из-за усиления при этом ионизации воздуха объёмный заряд вблизи провода пополняется и напряжённость поля в итоге сохраняется равной $IMAGE88$. Таким образом, вследствии непрерывного удаления объёмного заряда от провода коронный разряд может поддерживаться неограниченно долго.
При больших диаметрах проводов напряженность электрического поля в окрестности провода уменьшается значительно медленнее, чем вблизи проводов малого диаметра. Поэтому зона ионизации- ‘чехол’ короны – имеет большие размеры, и даже при начальном напряжении лавины могут достигать критической длины. Корона в этом случае возникает сразу в стримерной форме; структура зоны ионизации дискретна, светятся многочисленные стримерные каналы.
На проводах малых диаметров (до 1 см) корона возникает в лавинной форме. Зона ионизации достаточно однородна, свечение сосредоточено в узком чехле. Однако при увеличении напряжения сверх начального размеры зоны ионизации возрастут и корона из лавинной переходит в стримерную.
Ток стримерной короны состоит из отдельных импульсов с очень крутым фронтом (длительность фронта – порядка десятков наносекунд). Это высокочастотная составляющая тока корона является источником интенсивного электромагнитного излучения с широким спектром частот, которое создаёт помехи радио- телевизионному приёму. При коронировании проводов линий сверхвысокого напряжений может также возникать звуковой эффект, особенно сильный при дожде.
Объёмный заряд короны, образовавшийся в один из полупериодов перменного напряжения, за время до изменения полярности провода может переместится на несколько десятков сантиметров. Вследствие этого объёмные заряды обоих знаков совершают возвратно-поступательное движение вблизи провода, медленно удаляясь от него в область слабого поля, и там рекомбинируют. Только несущественная часть объёмного заряда может дойти до проводов соседних фаз. Вследствие этого процессы коронирования каждой из фаз трёхфазной линии не влияют друг на друга (эффект биполярности отсутствует), и каждая фаза может рассматриваться изолированно от других.
Для того чтобы исключить потери энергии на корону, а также и радиопомехи, начальное напряжение короны должно быть не ниже наибольшего рабочего напряжения линии относительно земли. Обеспечить это соотношение надлежащим выбором диаметра проводов можно только для условий сухой погоды. При атмосферных осадках исключить коронирование проводов невозможно.
Условие исключения короны: $IMAGE93$ принимая $IMAGE94$, $IMAGE95$ и $IMAGE96$ (характерное значение для линий $IMAGE97$), получаем $IMAGE98$
Для линий электропередач 110кВ наименьшие диаметры проводов, при которых исключается корона в хорошую погоду, оставляют $IMAGE99$.
При номинальных напряжениях 330 кВ и выше необходимы провода ещё большего диаметра, во многих случаях превышающий диаметр, выбранный из условия передачи по линий заданной мощности. В таких случаях целесообразно иметь провода, площадь поперечного сечения которых по проводящему материалу и диаметру независимы. Это так называемые расширенные провода. Они имеют диаметр, при котором обеспечивается необходимое снижение напряжённости поля на их поверхности, а для сокращения площади поперечного сечения делаются полыми или со стеклопластиковой сердцевиной.
Другое решение, получившее в настоящее время широкое распространение, было предложено ещё в 1910 г. Акад. В.Ф. Миткевичем и состоит в применении расщепленных проводов фаз. В этом случае каждая фаза линии состоит вместо одного провода большого диаметра из нескольких параллельных проводов относительно малого диаметра. В такой конструкции фазы удаётся при требуемом суммарном сечении проводов существенно уменьшить максимальную напряжённость поля на их поверхности.
При переменном напряжении корона зажигается в момент, когда напряжённость поля у провода достигнет значения $IMAGE88$, и горит, пока напряжение не достигнет максимума. После этого напряжённость поля у провода становится ниже $IMAGE88$, и корона потухает.
· Годовые потери на корону, $IMAGE102$
$IMAGE103$
· Среднегодовая мощность потерь, $IMAGE104$
$IMAGE105$
где n – число проводов во всех трёх фазах с учётом расщепления;
r – радиус провода в расщеплённой фазе;
Р – потери мощности при различных погодных условиях, км;
h – продолжительность отдельных видов погоды, час.
· Одним из способов оценки потерь энергии на корону является расчёт с использованием обобщённых характеристик потерь для разных погодных условий [1].
Они представлены в координатах:
$IMAGE106$,
где $IMAGE88$ – начальная напряжённость поля, $IMAGE108$;
$IMAGE109$ – максимальная напряжённость на поверхности провода,
учитывающая влияние заряда соседних проводов расщеплённой
фазы, $IMAGE108$.
· Для расщеплённых проводов при радиусах проводов $IMAGE111$ начальная напряжённость поля определяется по формуле:
$IMAGE112$
$IMAGE113$- коэффициент гладкости провода
а максимальная – по соотношению
$IMAGE114$,
где $IMAGE115$ – коэффициент, учитывающий усиление напряжённости поля
вследствие влияния зарядов на соседних проводах расщеплённой
фазы,
$IMAGE116$.
В этих формулах:
$IMAGE117$– средняя рабочая напряжённость электрического поля на поверхности
проводов расщеплённой фазы, $IMAGE108$,
$IMAGE119$;
UФ – фазное напряжение провода, кВ;
rо – радиус провода расщеплённой фазы, см;
rр – радиус расщепления, см,
$IMAGE120$;
S – среднегеометрическое расстояние между фазами, м.
Для горизонтального расположения фаз с расстоянием между фазами а, величина $IMAGE121$.
$IMAGE122$ – эквивалентный радиус расщеплённой фазы, см.
При расщеплении фазы на 4 провода радиус
$IMAGE123$см.
Средняя напряжённость электрического поля
$IMAGE124$ $IMAGE108$
Коэффицие