База рефератов

Задача №5.

Расчет статически неопределимой рамы методом сил

Для статически неопределимой Е-образной рамы с одной скользящей и двумя неподвижными опорами используя метод сил, формулу Мора и правило Верещагина необходимо определить реакции опор и построить эпюры моментов, поперечных и продольных сил

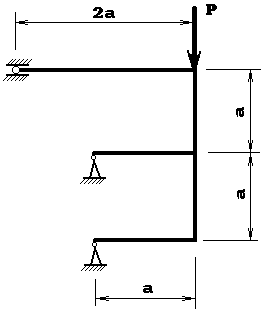
Построить эпюры M, Q и N.

Решение

Данная система дважды статически неопределима, так как рама прикреплена пятью связями, а уравнений статики для их определения – три. Выбираем основную систему путем отбрасывания лишних связей и заменой их неизвестными усилиями Х₁ и Х₂. Фактически Х₁ будет являться реакцией опоры С, а Х₂ – вертикальной составляющей реакции опоры В.

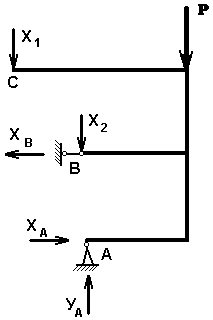
Составляем систему канонических уравнений метода сил:

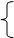d₁₁×Х₁ + d₁₂×Х₂ + D_1Р = 0;

d₂₁×Х₁ + d₂₂×Х₂ + D_2Р = 0.

Для определения коэффициентов при неизвестных и свободных членах необходимо построить эпюры изгибающих моментов поочередно для каждой силы.

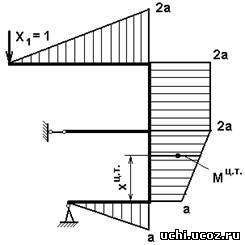
Эпюра единичных изгибающих моментов от единичной силы Х₁

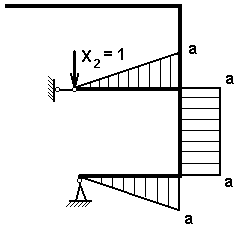
Эпюра единичных изгибающих моментов от единичной силы Х₂

$IMAGE6$

Грузовая эпюра от заданной нагрузки – силы Р.

Подсчитываем коэффициенты по формуле Мора используя правило Верещагина:

$IMAGE7$

где $IMAGE8$ – величина изгибающего момента единичной эпюры Х_j в точке, где расположен центр тяжести фигуры, образованной единичной эпюрой Х_i;

  $IMAGE9$ – площадь фигуры, образованной единичной эпюрой Х_i.

Например, для трапециевидного участка длиной L и размерами сторон м и М единичной эпюры Х₁ находим координату центра тяжести для трапеции:

$IMAGE10$;

Далее находим значение М^ц.т. в этой точке для всех эпюр.

– для эпюры Х₁ это будет:

$IMAGE11$,

– для эпюры Х₂ в любой точке данного участка М равно а, следовательно:

$IMAGE12$

– для эпюры Р это будет:

$IMAGE13$

Соответственно площади эпюр на данном участке будут равны:

$IMAGE14$

$IMAGE15$

$IMAGE16$

Аналогичным образом находим составляющие уравнения Мора для других, более простых участков и вычисляем требуемые коэффициенты:

$IMAGE17$

$IMAGE18$

$IMAGE19$

$IMAGE20$

$IMAGE21$

Подставив найденные коэффициенты в систему канонических уравнений и сократив на $IMAGE22$ и а³ получим систему двух уравнений с двумя неизвестными:

$IMAGE23$ $IMAGE23$ $IMAGE25$×Х₁ + $IMAGE26$×Х₂ + Р = 0; 56×Х₁ + 11×Х₂ + 6Р = 0;

$IMAGE26$×Х₁ + $IMAGE28$×Х₂ + $IMAGE29$×Р = 0.11×Х₁ + 10×Х₂ + 7Р = 0;

Вычитая из первого уравнения второе, получим более простое выражение, из которого выразим Х₂ и подставим затем во второе уравнение;

45Х₁ + Х₂ – Р = 0;®Х₂ = Р – 45Х₁;

11 Х₁ + 10Р – 450 Х₁ + 5Р = 0;

Х₁ = $IMAGE30$Р = 0,034Р;

Х₂ = Р – $IMAGE31$Р = – $IMAGE32$Р = –0,538Р;

Найдя значения неизвестных усилий Х₁ и Х₂, обратимся к основной системе и найдем Х_А, У_А и Х_В.

SУ = 0;

У_А – Х₁ – Х₂ – Р = 0;

У_А = Х₁ + Х₂ + Р = 0,034Р – 0,538Р + Р = 0,496Р;

SМ_А = 0;

Х₁×а + Х_В×а – Р×а = 0;

Х_В = Р – Х₁ = 0,966Р;

SХ = 0;

Х_А – Х_В = 0;

Х_А = Х_В = 0,966Р;

Зная значения всех усилий, действующих на раму, строим эпюры М, Q и N:

$IMAGE33$

$IMAGE34$

$IMAGE35$