Министерство образования и науки РФ
ГОУ ВПО «КЕМЕРОВСКИЙ ГОСУДАРСТВННЫЙ УНИВЕРСИТЕТ»
РЕФЕРАТ
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
Выполнила:
Студентка гр. Х-053
Тарасова К. В.
Проверила:
Журавлёва Л. В.
Кемерово, 2007
Содержание
Спектры щелочных металлов.................................................................................3
Рентгеновские лучи.................................................................................................8
Сплошной и дискретный спектры.........................................................................9
Закон Мозли и эффект экранирования ядра.......................................................10
Список литературы................................................................................................12
Спектры щелочных металлов
Спектры испускания атомов щелочных металлов, подобно спектру водорода, состоят из нескольких серий линий. Наиболее интенсивные из них получили названия: главная, резкая, диффузная и основная (или серия Бергмана). Эти названия имеют следующее происхождение. Главная серия названа так потому, что наблюдается и при поглощении. Следовательно, она соответствует переходам атома в основное состояние. Резкая и диффузная серии состоят соответственно из резких и размытых (диффузных) линий. Серия Бергмана была названа основной (фундаментальной) за своё сходство с сериями водорода.
Ещё в конце прошлого столетия Ридберг установил эмпирические формулы, позволяющие вычислить частоты серий щелочных металлов. Эти формулы для всех серий сходны и имеют вид:
ω = ω∞ -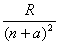 
,
где ω∞ - частота, соответствующая границе серии, R – постоянная Ридберга, n – целое число, а – дробное число.
Таким образом, частоты двух линий могут быть представлены как разности двух термов: постоянного и переменного, имеющего более сложный вид, чем бальмеровский терм R/n2. например. Спектральные серии натрия можно представить следующими формулами:
Резкая серия:
ω = S∞ - R/(n+s)2 (n = 4, 5,…)
Главная серия:
ω = P∞ - R/(n+p)2 (n = 3, 4,…)
Диффузная серия:
ω = D∞ - R/(n+d)2 (n = 3, 4,…)
Основная серия (серия Бергмана):
ω = F∞ - R/(n+f)2 (n = 4, 5,…)
При указанных значениях числа n константы в переменных термах имеют для натрия значения:
s = - 1,35
p = - 0,87
d = - 0,01
f = 0,00
Вследствие равенства константы f нулю переменный терм в формуле для основной серии совпадает с бальмеровским, а сама серия является водородоподобной.
С учётом сокращённых обозначений спектральные серии натрия могут быть представлены в следующем виде:
Резкая серия:
ω = 3P - nS
Главная серия:
ω = 3S - nP
Диффузная серия:
ω = 3P - nD
Основная серия:
ω = 3D – nF
Терм с точностью до постоянного множителя совпадает с энергией соответствующего состояния атома. Следовательно, каждому ряду спектральных термов должен соответствовать свой ряд энергетических уровней. Эмпирическая схема уровней атома натрия изображена на рис. 1. схемы уровней других щелочных металлов имеют такой же характер, как у натрия.
Схема уровней натрия отличается от схемы уровней водородного атома тем, что аналогичные уровни в различных рядах лежат на неодинаковой высоте. Несмотря на это отличие, обе схемы обнаруживают большое сходство. Это сходство даёт основание предположить, что спектры щелочных металлов испускаются при переходах самого внешнего ( так называемого валентного или оптического) электрона с одного уровня на другой.
Из рис. 1 видно, что энергия состояния оказывается зависящей, кроме числа n, также от того, в какой ряд попадает данный терм, т. е. от номера ряда термов. На схеме уровней атома водорода различные ряды термов (с совпадающими по высоте уровнями) отличаются значениями момента импульса электрона. Естественно предположить, что различные ряды термов щелочных металлов также отличаются значениями момента импульса оптического электрона. Поскольку уровни различных рядов в этом случае не лежат на одинаковой высоте, следует принять, что энергия оптического электрона в атоме щелочного металла зависит от величины момента импульса электрона (чего мы не наблюдали для водорода).
В более сложных, чем водород, атомах, имеющих несколько электронов, можно считать, что каждый из электронов движется в усредненном поле ядра и остальных электронов. Это поле уже не будет кулоновским (т. е. пропорциональным 1/r2), но обладает центральной симметрией (зависит только от r). В самом деле, в зависимости от степени проникновения электрона в глубь атома заряд ядра будет для данного электрона в большей или меньшей степени экранироваться другими электронами, так что эффективный заряд, воздействующий на рассматриваемый электрон, не будет постоянным. Вместе с тем, поскольку электроны движутся в атоме с огромными скоростями, усредненное по времени поле можно считать центрально-симметричным.
Решение уравнения Шредингера для электрона, движущегося в центрально-симметричном некулоновском поле, дает результат, аналогичный результату для водородного атома, с тем отличием, что энергетические уровни зависят не только от квантового числа n, но и от квантового числа l:
E = Enl
Ψ = ψnlm
Таким образом, в этом случае снимается вырождение по l. Отличие в энергии между состояниями с различными l и одинаковыми n вообще не так велико, как между состояниями с различными n. С увеличением l энергия уровней с одинаковыми n возрастает.
Числа l и n по-прежнему определяют момент импульса электрона и его проекцию на заданное направление.
Исследования оптических спектров ионов щелочных металлов показали, что момент импульса атомного остатка равен нулю. Следовательно, момент атома щелочного металла равен моменту его оптического электрона и L атома совпадает с l этого электрона. Поскольку при возбуждении атома и испускании света остальные электроны не изменяют своего энергетического состояния, схему уровней атома можно считать тождественной схеме уровней оптического электрона. Таким образом, квантовая механика объясняет все особенности приведённой на рис. 1 схемы.
На рис. 1 показаны переходы между уровнями, приводящие к возникновению различных серий. Эти переходы подчиняются правилу отбора: возможны лишь такие переходы, при которых момент атома изменяется на единицу: ∆L = ± 1
Рентгеновские лучи
Оптические спектры возникают при переходах слабее всего связанного с ядром оптического электрона из возбуждённого состояния в основное. Возбуждение атомов может происходить за счёт соударений между атомами, соударений атомов с электронами или за счёт поглощения фотонов.
При поглощении атомом порции энергии, достаточной для вырывания (или возбуждения) одного из внутренних электронов, испускается характеристическое рентгеновское излучение. Соответствующая порция энергии ожжет быть сообщена атому за счёт удара достаточно быстрым электроном или поглощения рентгеновского фотона.
В то время как тормозное рентгеновское излучение не зависит от материала антикатода и определяется лишь энергией бомбардирующих антикатод электронов, характеристическое излучение определяется природой вещества, из которого изготовлен антикатод. До тех пор пока энергия электрона недостаточна для возбуждения характеристического излучения, возникает только тормозное излучение. При достаточной энергии бомбардирующих электронов на фоне сплошного тормозного спектра появляются резкие линии характеристического спектра, причем интенсивность этих линий во много раз превосходит интенсивность фона.
Рентгеновские спектры отличаются заметной простотой. Они состоят из нескольких серий, обозначаемых буквами К, L, М, N и О. Каждая серия насчитывает небольшое число линий, обозначаемых в порядке убывания длины волны индексами: α, β, γ и т. д. Спектры разных элементов имеют сходный характер. При увеличении атомного номера Z весь рентгеновский спектр лишь смещается в коротковолновую часть, не меняя своей структуры. Это объясняется тем, что рентгеновские спектры возникают при переходах электронов во внутренних частях атомов, которые (части) имеют сходное строение.
Возбуждение атома состоит в удалении одного из внутренних электронов. Если под влиянием внешнего быстрого электрона или рентгеновского фотона вырывается один из двух электронов K-слоя, то освободившееся место может быть занято электроном из какого-либо внешнего слоя (L, М, N и т. д.). При этом возникает К-серия. Аналогично возникают и другие серии
Сплошной и дискретный спектр
Исследование показало, что тип спектра определяется характером светящегося объекта.
Сплошные спектры получаются в результате свечения твёрдых и жидких тел. Такие спектры дают и расплавленные металлы, а также светящиеся газы или пары, если они обладают значительной плотностью, т. е. находятся под очень высоким давлением. В частности, сплошной спектр Солнца представляет собой свечение паров высокой плотности.
Линейчатые и полосатые спектры характерны для свечения газов и паров малой плотности. Линейчатые спектры испускаются светящимися атомами. Многие газы состоят из отдельных атомов. Газы, состоящие из молекул, например, водород, кислород, пары йода и др., могут при возбуждении распадаться на атомы. Такие атомарные газы дают линейчатые спектры. Но можно вызвать свечение и целых молекул, не разбивая их на атомы. В таком случае испускаются полосатые спектры. При возбуждении таких многоатомных газов или паров нередко происходит частичная диссоциация и наблюдается одновременно и линейчатый и полосатый спектр.
Свечение атомов и молекул можно вызвать нагреванием. Если повышать давление светящегося пара или газа, то спектральные линии начинают расширяться, захватывая больший спектральный интервал. При очень больших давлениях (сотни и больше атмосфер0 линейчатый спектр постепенно переходит в сплошной, характерный для сжатых газов.
Закон Мозли и эффект экранирования ядра
Мозли (1913) установил простой закон, связывающий частоты спектральных линий с атомным номером испускающего их элемента:
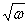= С(z - 
)
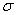Закон Мозли можно сформулировать следующим образом: корень квадратный из частоты является линейной функцией атомного номера. Константа 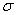сохраняет своё значение в пределах одной и той же серии для всех элементов, но меняется при переходе от одной серии к другой. По измерениям Мозли 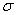= 1 для К-серии и 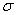= 7,5 для L-серии. Константа С имеет своё значение для каждой линии, одинаковое, однако, для всех элементов.
Зависимость, установленная Мозли, позволяет по измеренной длине волны рентгеновских линий точно установить атомный номер данного элемента.
Мозли дал простое теоретическое объяснение найденного им закона. Он установил, что для линии Кα константа С имеет значение, равное $IMAGE8$, где R – постоянная Ридберга. Следовательно, для этой линии
ω = R(Z – 1)2 $IMAGE9$ - $IMAGE10$
Линия такой же частоты получается при переходе электрона, находящегося в поле заряда (Z – 1)e, с уровня 2 на уровень 1.
Смысл константы σ легко понять: электроны, совершающие переход при испускании рентгеновских лучей, находятся под воздействием ядра, притяжение которого несколько ослаблено действием остальных окружающих его электронов. Это так называемый эффект экранирования ядра, находит своё выражение в необходимости вычесть из Z некоторую величину σ.
На какой-либо электрон одной из внутренних оболочек дальше отстоящие от ядра электроны воздействуют слабо, т. к. создаваемое ими внутри поле в среднем равно нулю. Поэтому внутренние электроны находятся в основном лишь под воздействием поля ядра и электронов, находящихся ближе к ядру. Таким образом, поправка σ вызывается наличием более глубоких электронов и слабым возмущением со стороны остальных электронов.
Список литературы
1. Элементарный учебник физики. Под редакцией Г. С. Ландсберга. Том 3 – М.: Наука, 1972 г.
2. Курс общей физики, том 3. Оптика, атомная физика, физика атомного ядра и элементарных частиц. Савельев И. В. – М.: Наука, 1971 г.
