Московский государственный технический университет им. Н.Э. Баумана.
Калужский филиал
“Квантовая статистика”
СОДЕРЖАНИЕ
Квантовая статистика. 3
Принцип тождественности. 3
Принцип Паули на неё не распространяется. 5
Формулы Ричардсона и Ричардсона-Дэшмана. 11
Литература.. 15
Квантовая статистика исследует физические свойства систем одинаковых микрочастиц, например, электронов, фотонов,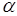 
- частиц и т.д.
Поведение совокупности частиц одного сорта описывается волновой функцией
(1)
q1,q2 - обобщённые координаты.
Квантовая статистика систем одинаковых микрочастиц допускает два класса функций: симметричные, сохраняющие свой знак при перестановке двух частиц:
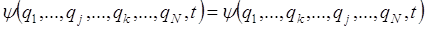
антисимметричные, меняющие знак при перестановке:
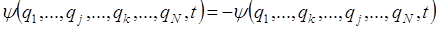
Эти два класса функций не могут переходить друг в друга.
Принцип тождественности: частицы одного и того же сорта не могут иметь никаких различимых особенностей. Потому взаимная перестановка двух одинаковых частиц не изменяет физического состояния системы.
В квантовой теории доказывается, что волновая функция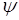 
всегда остаётся симметричной или антисим-метричной, т.е. какой она была в начальном состоянии.
Принадлежность частиц к тому или иному классу зависит от величины их собственного момента, иначе - спина.
Частицы, спин которых равен полуцелому числу квантов действия Планка $IMAGE6$ $IMAGE7$, описывается антисимметричными 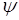- функциями. Эти частицы называются частицами Ферми, или фермионами, а описывающая их статистика называется статистикой Ферми-Дирака.
Электроны, позитроны, протоны, нейтроны, атомы, ионы, атомные ядра, состоящие из нечётного числа элементарных частиц, имеют полуцелый спин. Все они описываются статистикой Ферми-Дирака.
Например: статистике Ферми-Дирака подчиняются
$IMAGE9$ $IMAGE10$ $IMAGE11$ $IMAGE12$ $IMAGE13$
Частицы с целочисленным спином $IMAGE14$, описываются симметричными 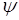- функциями. Они называются частицами Бозе или бозонами. Применяемая к ним статистика называется статистикой Бозе-Эйнштейна. Ей подчиняются микрочастицы, состоящие из чётного числа элементарных частиц.
Например:
$IMAGE16$ $IMAGE17$ $IMAGE18$ $IMAGE19$
ядра дейтерия $IMAGE20$
имеют спин, равный целому числу постоянных Планка $IMAGE21$. Частицы света (фотоны) имеют спин, равный нулю.
В квантовой механике частицы неразличимы.
Принцип Паули следует из свойств антисимметричных волновых функций в данном квантовом состоянии может находиться только одна микрочастица.
Классические частицы подчиняются статистике Максвелла-Больцмана.
Три статистики.
Две квантовые и одна классическая статистика
Максвелла-Больцмана.
4 состояния, частицы различимы, энергия может иметь как: дискретный, так и непрерывный спектр. Ей соответствует функция распределения Максвелла-Вольцмана
$IMAGE22$
Статистика Бозе-Эйнштейна:
Частицы неразделимы, целый спин. Принцип Паули не распространяется. Ей соответствует функция распределения Бозе-Эйнштейна. Энергия дискретна.
$IMAGE23$
Статистика Ферми-Дирака:
Частицы неразличимы, полуцелый спин, принцип Паули: в одном квантовом состоянии не может быть больше одной частицы. Каждое квантовое состояние либо заполнено единственной микрочастицей, либо не заполнено. Энергия дискретна. Ей соответствует функция Ферми-Дирака
$IMAGE24$ $IMAGE25$
Итак свойства твёрдых тел определяются свойством электронного газа, т.е. статистикой Ферми-Дирака, которая изучает свойства систем, состоящих из большого числа частиц. Важное значение имеет функция распределения частиц по энергиям n(E). Через dn обозначают число частиц в единице объёма, энергия которых заключена в бесконечно узком интервале энергии от Е до E+dE.
dn=n(E) dE (1)
Функция n(E) позволяет рассчитать число частиц в единице объёма, энергия которых заключена в конечном интервале от E1 до E2.
$IMAGE26$ (2)
Если через n0 обозначить общее число частиц в единице объёма безотносительно к значению их энергий, т.е. концентрацию частиц, то из (2) вытекает следующее условие нормировки для функции распределения:
$IMAGE27$ (3)
Различные частицы системы имеют различные значения энергии, причём функция n(E) характеризует распределение частиц по энергиям. Зная n(E), можно рассчитать среднее значение энергии частиц данной системы:
$IMAGE28$ (4) или $IMAGE29$ (5)
Зная функцию распределения частиц по энергиям, можно найти среднее значение любой физической величины А(Е), зависящей от энергии частицы, Например, скорость частицы
$IMAGE30$
Среднее значение А(Е) в системе частиц с известной функцией распределения n(E) определяется по формуле:
$IMAGE31$ (6)
В классической статистике Максвелла-Больцмана, которая применима к классическому газу, эта функция распределения зависит от значений абсолютной температуры газа Т и имеет вид:
$IMAGE32$ (7)
В квантовой статистике Ферми-Дирака, которая применима к системе квантовых частиц, имеющих полуцелый спин и подчиняется принципу запрета Паули (мелкие частицы, как электроны, протоны, нейтроны и др., называются фермионами), функция распределения имеет вид произведения двух функций:
$IMAGE33$ (8)
где $IMAGE34$ (9)
$IMAGE35$ (10)
$IMAGE36$ $IMAGE37$
m - масса частицы
Функция g(E) характеризует число квантовых состояний в единице объёма в единичном интервале для свободных частиц и носит название плотности квантовых состояний. Из (9) следует, что плотность квантовых состояний для свободных частиц, подчиняющихся статистике Ферми-Дирака, растет с ростом энергии:
$IMAGE24$g(E) ~ $IMAGE39$
Функция f(E,T) называется функцией Ферми. Эта функция определяется вероятностью того, что квантовые состояния с энергией Е заняты частицами при заданной температуре Т. По её смыслу её не может быть больше единицы.
Параметр системы частиц EF, входящий в выражение для функции Ферми, носит название энергии Ферми (энергию Ферми называют также химическим потенциалом), а соответствующее значение по лекалу энергий называется энергией Ферми.
Формально, исходя из (10), энергию Ферми можно определить как энергию таких квантовых состоянии, вероятность заполнения которых частицами равна 0,5. Действительно, из (10) следует, что f(EF,T) =0,5.
Энергия Ферми квантовой системы фермионов зависит от
$IMAGE40$ (11)
концентрации частиц n0 и от температуры Т, а значение энергии Ферми при абсолютном нуле температуры (здесь и далее абсолютный нуль температуры понимается как предел Т=>0, имеется в виду, что абсолютный нуль недостижим) $IMAGE41$ можно рассматривать по формуле
$IMAGE42$
$IMAGE43$.
Обычно рассматриваются системы, у которых $IMAGE44$. Для таких систем cогласно (1) можно пренебречь зависимостью энергии Ферми от температуры и считать
$IMAGE45$
Вид функции Ферми приведен на рисунке.
$IMAGE46$
полностью заполненные частицами, а все квантовые состояния с энергией $IMAGE47$ - пустые. Поэтому энергию Ферми при абсолютном нуле $IMAGE41$ можно определить как максимальную энергию частиц данной системы при T=00K. За счет нагрева системы часть частиц имевших при T=00K энергии меньше уровня Ферми приобретают энергии несколько выше уровня Ферми. При этом область частично заполненных квантовых состояний, т.е. область, где, $IMAGE49$, имеет по шкале энергий размер порядка 2КТ.
Системы, описываемые квантовой статистикой Ферми-Дирака, называют вырожденными системами, в отличие от невырожденных систем классических частиц, подчиняющихся статистике Максвелла-Больцмана.
$IMAGE22$
При температурах выше некоторой температуры TB, которая называется температурой вырождения системы, свойства системы фермионов изменяются так, что квантовая статистика Ферми-Дирака при Т>TB переходит в классическую статистику Максвелла-Вольцмана. При температуре выше температуры вырождения часть фермионов можно рассматривать как невырожденный классический газ. Температура вырождения системы зависит от ее энергии Ферми, т.е. от концентрации частиц n0, увеличиваясь с ростом n0.
$IMAGE51$
Например, температура вырождения в калии, $IMAGE52$;
$IMAGE53$.
$IMAGE54$.
$IMAGE55$.
Такие большие значения для температур вырождения электронного газа (порядка десятков тысяч градусов) получаются практически для всех металлов. Это говорит о том, что электронный газ в металле практически всегда следует рассматривать как вырожденный газ. Классическое описание его свойств с применением статики Максвелла-Больцмана невозможно.
Зная распределение dn(E) электронов в металле, можно установить распределение dn(P) электронов, по импульсам. Определим частичный случай распределения при Т=О.
$IMAGE56$,
$IMAGE57$
$IMAGE58$.
$IMAGE59$.
$IMAGE60$
$IMAGE61$
При T=0, f(E,0) =1.
$IMAGE62$
Работа выхода электрона из металла. Термоэлектронная эмиссия.
Высокая электропроводимость металлов говорит о том, что электроны способны сравнительно свободно перемещаться внутри всей кристаллической решетки металла.
Затруднен их выход из металла, в вакуум, требующей затраты некоторой энергии, называемой 'работой выхода'.
Это навело на мысль рассматривать металл в первом приближении, просто как потенциальную яму, внутри которой (т.е. в металле) потенциальная энергия электрона равна нулю U0=0, а вне металла, т.е. в вакууме U>0. Эта упрощенная модель позволила объяснить многие явления.
Работа выхода - энергия, которую нужно затрачивать, чтобы энергия электрона стала больше высоты потенциального барьера в поверхностном слое металла. И благодаря туннельному эффекту электрон может покинуть металл.
$IMAGE63$
По принципу Паули на каждом энергетическом уровне может находится max два электрона с противоположными спинами (два квантовых состояния).
$IMAGE64$верхняя граница заполненных уровней при T=0 (уровень Ферми).
$IMAGE65$ - максимальный импульс при Т=0.
$IMAGE66$
Для серебра
$IMAGE67$ - плотность серебра.
A=107,9 - атомный вес (а. е. м).
$IMAGE68$
$IMAGE69$ или $IMAGE70$
Работа выхода $IMAGE71$
Глубина потенциальной ямы $IMAGE72$, с квантовой точки зрения работа выхода равна разности высоты потенциального барьера и энергии Ферми
$IMAGE73$
$IMAGE74$
Работа выхода характеризует минимальную энергию, которую надо сообщить свободному электрону, находящемуся на уровне Ферми, чтобы он мог преодолеть потенциальный барьер на поверхности твердого тела и выйти за пределы металла,
При комнатной температуре число электронов, энергия которых достаточна для преодоления этого барьера, очень невелика. Однако их число резко возрастает с повышением температуры.
Явление испускания электронов нагретыми телами, называется термоэлектронной эмиссией.
Расчет плотности тока термоэлектронной эмиссии при некоторой температуре Т для металла с работой выхода А. определяется формулой Ричардсона - Дэшмана:
$IMAGE75$, где
C=Const= $IMAGE76$
Экспоненциальный множитель
$IMAGE77$
для A>>KT определяет вероятность того, что электрон в металле при температуре Т имеет энергию Uo, достаточную, чтобы покинуть металл, преодолев потенциальный барьер вблизи поверхности металла. Все эти выводы получены с точки зрения квантовой статистики Ферми-Дирака для электронного газа, т.е. для частиц, имеющих полуцелый спин и подчиняющихся принципу Паули.
Дэшман получил формулу исходя из квантовых представлений в 1923г. а Ричардсон вывел в 1901г исходя из классических представлений.
Так эмиссия определяется
$IMAGE78$
Изменение тока связанно с изменением температуры $IMAGE79$
$IMAGE80$
$IMAGE81$
$IMAGE82$
Литература 1. Шпольский Э.В. "Атомные физика". т. I-II М. Наука, 1984 г.
2. Блохинцев Д.И. "Основы Квантовой механики" М. Наука, 1983 г.
3. Гольдин