Элементы теории представлений
1. Основы теории представлений. Различные представления волновой функции (различные представления состояний)
2. Обозначения Дирака
3. Преобразование операторов от одного представления к другому
Введение
Для создания новой физической теории необходимо cформулировать систему постулатов, найти математический аппарат, соответствующий физическому смыслу рассматриваемых проблем и установить связь физических фактов с математическим формализмом.
Для формулировки ньютоновской механики потребовалось развитие дифференциального и интегрального исчисления. В 20-м столетии произошли серьезные изменения в представлениях физиков о математических основах их науки. Закономерности микромира коренным образом отличаются от законов макроскопического мира, объектами которого мы являемся.
Одно из основных понятий квантовой механики – понятие состояния квантово-механической системы. Смысл этого понятия в квантовой и классической физике различен. Содержание понятия состояния квантово-механической системы будет выясняться постепенно в процессе изучения.
Информацию о состоянии системы получают в процессе измерения, т.е. при взаимодействии квантовой системы с макроскопическим прибором. Поэтому результаты измерения характеризуются теми же физическими величинами, которые используются в классической макроскопической физике. Физические величины в квантовой механике часто называют динамическими переменными или наблюдаемыми. В квантовой механике физические величины имеют иную математическую природу, чем в классической, потому что состояния квантово-механической системы и динамические переменные "взаимосвязаны весьма странным образом, который непостижим с классической точки зрения". [1, c31].
В квантовой механике изучаются такие явления, которые не могут быть объяснены с помощью известных ранее понятий. Ведь наш язык – это "слепок с обыденного опыта человека, он никогда не сможет выйти за пределы этого опыта. Классическая физика как раз и ограничивается рассмотрением явлений, которые имеют в языке адекватный словесный эквивалент".[1]
При изучении явлений, происходящих на ином структурном уровне организации материи, на помощь приходит другой язык – математика. "Математика есть орудие, специально приспособленное для овладения всякого рода абстрактными понятиями и в этом отношении ее могущество беспредельно". [1, c13]. "Тем не менее, – считает П. Дирак, – математика есть лишь орудие, и нужно уметь владеть физическими идеями безотносительно к их математической форме". (Там же). Выбор математических методов, адекватных физической сущности задачи, возможно более полное прослеживание аналогий между понятиями и методами математики и физики способствует формированию современного физического мышления. В то же время освоение абстрактных математических объектов возможно только при их реализации физическими объектами.
Для описания квантовых свойств материи может быть использован различный математический аппарат. В 1925г. Вернером Гейзенбергом была создана матричная механика. В этом же году, но немного позже, Э. Шрёдингер создал волновую механику. Он доказал также, что обе формулировки эквивалентны. Наиболее изящная формулировка квантовой механики создана в 1930г английскими физиком П. Дираком. Именно эта формулировка сейчас чаще всего используется. Все формулировки квантовой механики эквивалентны, могут быть преобразованы друг в друга и приводят к одинаковым физическим результатам.
1. Основы теории представлений. Различные представления волновой функции (различные представления состояния)
Состояния квантово-механической системы характеризуется волновой функцией или амплитудой вероятности. Независимые переменные, функцией которой она является, могут быть различными. Например, декартовы координаты системы
,
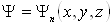значения ее импульса
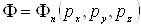
и т. п. Буквы, обозначающие независимые переменные, называют индексом представления. Индекс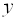 
волновой функции (в данном случае 
) обозначает набор значений физических величин или соответствующих квантовых чисел, которые характеризуют данное состояние. Поэтому этот индекс обычно называют индексом состояния.
Если волновая функция зависит от координат, то описание состояния с помощью такой функции называют координатным представлением. Например, для свободной частицы, движущейся вдоль оси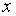 
, в координатном представлении.
$IMAGE6$
Волновую функцию $IMAGE7$, характеризующую состояние системы, можно разложить в ряд по собственным функциям оператора динамической переменной $IMAGE8$. Если этот оператор имеет дискретный спектр собственных значений, т. е.
$IMAGE9$, то
$IMAGE10$
Коэффициенты разложения определяются из выражения
$IMAGE11$
(Здесь, как и раньше, $IMAGE12$ – произведение дифференциалов независимых переменных). В § 2.4.2 был выяснен физический смысл этих коэффициентов: $IMAGE13$ есть вероятность того, что в состоянии, описываемым $IMAGE7$-функцией, физическая величина, представляемая оператором $IMAGE15$, имеет значение $IMAGE16$. Таким образом $IMAGE17$ имеет смысл амплитуды вероятности, если независимой переменной является величина $IMAGE18$. Совокупность амплитуд $IMAGE19$ является волновой функцией в $IMAGE20$ $IMAGE18$- представлении. Эту совокупность можно представить в виде матрицы с одним столбцом
$IMAGE22$
Если спектр собственных значений оператора непрерывный, то аналогично имеем
$IMAGE23$
$IMAGE24$
Пример 1. Записать скалярное произведение двух функций $IMAGE25$ и $IMAGE26$ в $IMAGE20$ $IMAGE28$- представлении.
Компоненты $IMAGE25$ и $IMAGE26$ в $IMAGE20$ $IMAGE28$- представлении находим, раскладывая эти функции в ряд по собственным функциям оператора $IMAGE33$:
$IMAGE34$, (Ι)
$IMAGE35$ (ΙΙ)
$IMAGE36$ (ΙΙΙ) $IMAGE37$ (ΙV).
Подставляем разложение (Ι) и (ΙΙ) в скалярное произведение функций:
$IMAGE38$.
Меняя местами знаки суммирования и интегрирования и учитывая ортонормированность собственных функций оператора $IMAGE33$ получаем:
$IMAGE40$.
Чтобы получить такое выражение по правилу умножения матриц, следует перемножить матрицу-строку
$IMAGE41$ (V)
на матрицу-столбец (ΙΙΙ):
$IMAGE41$ $IMAGE43$
Матрица (V) транспонирована по отношению к матрице (ΙV) и ее элементы комплексно сопряжены с элементами последней. Такая матрица называется сопряженной с $IMAGE44$ и обозначается $IMAGE45$. Таким образом, комплексно сопряженной функции под знаком интеграла соответствует сопряженная матрица.
2. Обозначения Дирака
Проведена аналогия между собственными функциями эрмитовых операторов и ортами прямоугольных координатных осей. Продолжим ее обсуждение.
Вектор $IMAGE46$ в $IMAGE47$- мерном пространстве задается совокупностью $IMAGE47$, вообще говоря, комплексных величин, называемых компонентами этого вектора
$IMAGE49$
Аналогия между соотношениями и очевидна. Выражение определяет вектор через его проекции на оси координат в многомерном пространстве. Выражение является разложением $IMAGE7$-функции по собственным функциям некоторого оператора. Систему ортонормированных собственных функций $IMAGE51$, следовательно, можно рассматривать как базис в бесконечномерном пространстве, а величины $IMAGE52$ – как компоненты $IMAGE7$-функции по осям этого базиса. В зависимости от выбора базиса (т. е. от выбора системы собственных функций, следовательно, от выбора представления) получается та или иная совокупность компонент $IMAGE52$.
Переход от одного представления к другому геометрически означает переход от системы координат, образованных базисными векторами (собственными функциями) одного оператора к системе координат, образованных базисными векторами (собственными функциями) другого оператора. Таким образом, квантовое состояние микрообъекта не обязательно должно характеризоваться волновой функцией в реальном пространстве. Квантовое состояние не сводится к одной какой-то совокупности амплитуд вероятности
$IMAGE55$
и т. п. Каждая из этих совокупностей отражает одну из сторон понятия квантового состояния и является одной из возможных его реализаций. Аналогично, вектор в $IMAGE47$- мерном евклидовом пространстве может быть представлен совокупностью его проекций в различных системах координат:
$IMAGE49$, $IMAGE58$
и т. п. Здесь $IMAGE59$ – базисные векторы (орты), например, в сферической системе координат, $IMAGE60$ – в декартовой.
Данная аналогия привела П. Дирака к мысли характеризовать состояние системы вектором состояния в бесконечномерном гильбертовом пространстве. Вектор состояния он предложил обозначать символом $IMAGE61$. В середине скобки, по Дираку, должен помещаться индекс состояния, т. е. величина или набор величин, которые определяют состояние системы. Например, если система находится в состоянии с энергией $IMAGE62$, то записывают $IMAGE63$ или $IMAGE64$. Этот вектор состояния называют кэт-вектором. Он характеризует состояние системы независимо от выбора представления. Кэт-вектору сопоставляется бра-вектор, обозначаемый зеркально отраженной скобкой $IMAGE65$. Бра-вектор связан с кэт-вектором соотношением $IMAGE66$= $IMAGE67$+. Например, если совокупность компонент кэт-вектора представлена в виде матрицы
$IMAGE68$= $IMAGE69$, то $IMAGE70$= $IMAGE68$+= $IMAGE72$.
Внутри скобки $IMAGE65$ помещается индекс представления. Например, $IMAGE74$| означает, что используется координатное представление. Скалярное произведение кэт и бра-векторов обозначается полным скобочным выражением $IMAGE75$и представляет собой число. Например, волновая функция $IMAGE76$ в $IMAGE77$- представлении с помощью скобок записывается так: $IMAGE78$. Волновая функция свободной частицы, находящейся в состоянии $IMAGE79$ определенным значением импульса $IMAGE80$ в координатном представлении (время фиксировано):
$IMAGE81$,
Название «бра» и «кэт» соответствуют двум частям английского слова «bracket» (скобка).
Волновая функция (амплитуда вероятности), как известно, характеризует вероятность результатов измерений, проводимых над системой. Скобочное выражение $IMAGE75$ составлено так, что справа указывается начальное состояние, а слева – то, в которое переходит система при измерении, т. е. конечное. Таким образом, скобочная запись читается справа налево. Например, $IMAGE83$ $IMAGE84$ есть амплитуда вероятности того, что система будет иметь координату $IMAGE85$, если она находится в состоянии характеризуемом импульсом $IMAGE80$.
Уравнение собственных значений в обозначениях П. Дирака можно записать в виде:
$IMAGE87$
Здесь собственный вектор состояний $IMAGE88$ обозначается той же буквой, что и соответствующее собственное значение. Запишем, пользуясь этими обозначениями, выражение. Пусть $IMAGE89$ вектор состояния системы, а $IMAGE88$ – базисная система векторов. Тогда
$IMAGE7$>= $IMAGE92$, где $IMAGE93$
Вектор состояния системы – понятие более абстрактное, чем волновая функция. В зависимости от выбора независимых переменных (представления) вектору состояния $IMAGE94$ могут соответствовать различные волновые функции: в координатном представлении – $IMAGE95$, в импульсном – $IMAGE96$, в энергетическом – $IMAGE97$ и т.д. Т.е. волновая функция есть проекция вектора состояния на соответствующий базисный вектор.
Получим в обозначениях Дирака условие полноты ортонормированного базиса. Оно часто бывает полезным при использовании этого формализма.
Пусть $IMAGE98$ - единичный оператор, который любому вектору состояния $IMAGE99$ ставит в соответствие тот же вектор:
$IMAGE100$
Представим $IMAGE101$ в виде разложения по ортонормированному базису $IMAGE102$ (т.е. по системе собственных векторов оператора $IMAGE103$):
$IMAGE104$
Подставляем это разложение в:
$IMAGE105$
В силу произвольности вектора $IMAGE106$ получаем
$IMAGE107$
Это соотношение и является условием полноты в обозначениях Дирака.
Пример. Записать в обозначениях Дирака среднее значение физической величины представленной оператором $IMAGE103$, если состояние системы характеризуется вектором состояния $IMAGE99$. (Спектр собственных значений оператора $IMAGE103$ считать дискретным).
Среднее значение дискретной случайной величины равно сумме произведений ее возможных значений на их вероятности:
$IMAGE111$
Здесь $IMAGE112$ - собственные значения оператора $IMAGE113$, $IMAGE102$ - его собственные векторы и $IMAGE115$ - волновая функция системы в $IMAGE18$- представлении. Преобразуем выражение для среднего значения, пользуясь свойством скалярного произведения
$IMAGE117$
$IMAGE118$
В последнем преобразовании использовано условие полноты
Таким образом, в обозначениях Дирака
$IMAGE119$
квантовый представление волновой состояние
3. Преобразование операторов от одного представления к другому
Пусть оператор $IMAGE103$ задан в координатном представлении и переводит функцию $IMAGE121$ в функцию $IMAGE122$: