Дипломна робота. Факторізації чотирьохмірних симплектичних груп
Зміст
1.Введення
2.Перелік умовних позначок
3. Основні поняття
4. Ізометрії
5. Проективні перетворення
6. Структурні теореми. Порядки симплектичних груп
7. Центри
8. Комутанти
9. Теореми про простоту
10. Основні результати
Висновок
Список використаних джерел
1.Введення Кінцева група  допускає факторізацію, якщо
допускає факторізацію, якщо  для деяких підгруп
для деяких підгруп 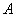 і
і 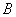 групи
групи  . При цьому виникають дві задачі: які факторізації допускає задана група
. При цьому виникають дві задачі: які факторізації допускає задана група  і як будова співмножників
і як будова співмножників 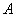 і
і 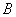 впливає на будову самої групи
впливає на будову самої групи  . Природно, що вивчення кінцевих груп, що володіють факторізацією, дає можливість глибше зрозуміти будову кінцевої групи. Дана тематика вивчалася такими видними математиками як Ф. Хол, С.А. Чунихин, Х. Виландт, Л.С. Казарін, Д.И. Зайцев, С.А. Сискин і ін. Ними був доведений ряд глибоких результатів у теорії кінцевих груп. Аналогічні задачі виникають і в інших розділах математики (наприклад, в алгебрах Чи).
. Природно, що вивчення кінцевих груп, що володіють факторізацією, дає можливість глибше зрозуміти будову кінцевої групи. Дана тематика вивчалася такими видними математиками як Ф. Хол, С.А. Чунихин, Х. Виландт, Л.С. Казарін, Д.И. Зайцев, С.А. Сискин і ін. Ними був доведений ряд глибоких результатів у теорії кінцевих груп. Аналогічні задачі виникають і в інших розділах математики (наприклад, в алгебрах Чи).
Після завершення класифікації кінцевих простих неабелевих груп актуальної стала задача одержання факторизаций конкретних простих неабелевих груп і, зокрема, простих груп лієвського типу малого лієвського рангу. Дані питання розглядалися Н. Іто, що одержав всі факторізації лінійних груп лієвського рангу 1 над кінцевим полем Галуа, а також С. Блаумом, що описали факторізації лінійних і унітарних груп розмірності 3.
У дипломній роботі розглянуті факторізації чотирьохмірних симплектичних груп. Для таких груп знайдені всі максимальні факторізації.
2.Перелік умовних позначок У роботі всі розглянуті групи передбачаються кінцевими. Буквами $IMAGE10$ позначаються прості числа.
Будемо розрізняти знак включення множин $IMAGE11$ і знак строгого включення $IMAGE12$;
$IMAGE13$ і $IMAGE14$ - відповідно знаки перетинання й об'єднання множин;
$IMAGE15$ - потужність множини $IMAGE16$;
$IMAGE17$ - порожня множина;
$IMAGE18$ - множина всіх простих чисел;
$IMAGE19$ - деяка множина простих чисел, тобто $IMAGE20$;
$IMAGE21$ - доповнення до $IMAGE19$ у множині всіх простих чисел; зокрема, $IMAGE23$;
Нехай  - група. Тоді:
- група. Тоді:
$IMAGE25$ - порядок групи  ;
;
$IMAGE27$ - порядок елемента $IMAGE28$ групи  ;
;
$IMAGE30$ - одиничний елемент і одинична підгрупа групи  ;
;
$IMAGE32$ - множина всіх простих дільників порядку групи  ;
;
$IMAGE34$ - множина всіх різних простих дільників натурального числа $IMAGE35$;
$IMAGE19$ - група - група  , для якої $IMAGE38$;
, для якої $IMAGE38$;
$IMAGE39$ - група - група  , для якої $IMAGE41$;
, для якої $IMAGE41$;
$IMAGE42$ - підгрупа Фратіні групи  , тобто перетинання всіх максимальних підгруп
, тобто перетинання всіх максимальних підгруп  ;
;
$IMAGE45$ - найбільша нормальна розв'язна підгрупа групи  ;
;
$IMAGE47$ - найбільша нормальна $IMAGE39$--підгрупа групи  ;
;
$IMAGE50$ - найбільша нормальна $IMAGE19$--підгрупа групи  ;
;
$IMAGE53$ - $IMAGE19$--холовська підгрупа групи  ;
;
$IMAGE56$ - силовська $IMAGE39$--підгрупа групи  ;
;
$IMAGE59$ - доповнення до силовської $IMAGE39$--підгрупи в групі  , тобто $IMAGE62$--холовська підгрупа групи
, тобто $IMAGE62$--холовська підгрупа групи  ;
;
$IMAGE64$ - $IMAGE65$ є підгрупою групи  ;
;
$IMAGE67$ - $IMAGE65$ є власною підгрупою групи  ;
;
$IMAGE70$ - $IMAGE71$ є максимальною підгрупою групи  ;
;
$IMAGE73$ - $IMAGE65$ є нормальною підгрупою групи  ;
;
$IMAGE76$ - $IMAGE77$ є мінімальною нормальною підгрупою групи  ;
;
$IMAGE79$ - індекс підгрупи $IMAGE65$ в групі  ;
;
$IMAGE82$;
$IMAGE83$ - централізатор підгрупи $IMAGE65$ в групі  ;
;
$IMAGE86$ - нормалізатор підгрупи $IMAGE65$ в групі  ;
;
$IMAGE89$ - центр групи  ;
;
$IMAGE91$ - циклічна група порядку $IMAGE35$;
Якщо $IMAGE93$, то $IMAGE94$.
Якщо $IMAGE95$, $IMAGE96$, то $IMAGE97$.
Класи груп, тобто сукупності груп, замкнуті відносно ізоморфізмов, позначаються прописними готичними буквами. За деякими класами закріплені стандартні позначення:
$IMAGE98$ - клас всіх груп;
$IMAGE99$ - клас всіх розв'язних груп.
3. Основні поняття Групою називається непуста множина  з бінарною алгебраїчною операцією (множенням), що задовольняє наступною вимогою:
з бінарною алгебраїчною операцією (множенням), що задовольняє наступною вимогою:
1) операція визначена на  , тобто $IMAGE102$ для всіх $IMAGE103$;
, тобто $IMAGE102$ для всіх $IMAGE103$;
2) операція асоціативна, тобто $IMAGE104$ для будь-яких $IMAGE105$;
3) в  існує одиничний елемент, тобто такий елемент $IMAGE107$, що $IMAGE108$ для всіх $IMAGE109$, що $IMAGE108$ для всіх $IMAGE109$;
існує одиничний елемент, тобто такий елемент $IMAGE107$, що $IMAGE108$ для всіх $IMAGE109$, що $IMAGE108$ для всіх $IMAGE109$;
4) кожний елемент володіє зворотним, тобто для кожного $IMAGE109$ існує такий елемент $IMAGE113$, що $IMAGE114$.
Більш коротко: напівгрупа з одиницею, у якій кожний елемент володіє зворотним, називається групою.
Групу з комутативною операцією називають комутативною або абелевої. Якщо  - кінцева множина, що є групою, то
- кінцева множина, що є групою, то  називають кінцевою групою, а число $IMAGE25$ елементів в
називають кінцевою групою, а число $IMAGE25$ елементів в  - порядком групи
- порядком групи  .
.
Підмножина $IMAGE65$ групи  називається підгрупою, якщо $IMAGE65$ - група щодо тієї ж операції, що визначена на
називається підгрупою, якщо $IMAGE65$ - група щодо тієї ж операції, що визначена на  . Запис $IMAGE64$ означає, що $IMAGE65$ - підгрупа групи
. Запис $IMAGE64$ означає, що $IMAGE65$ - підгрупа групи  , а $IMAGE67$ - що $IMAGE64$ - власна підгрупа групи
, а $IMAGE67$ - що $IMAGE64$ - власна підгрупа групи  , тобто $IMAGE64$ й $IMAGE131$.
, тобто $IMAGE64$ й $IMAGE131$.
Теорема 1 Непуста підмножина $IMAGE65$ групи  буде підгрупою тоді й тільки тоді, коли $IMAGE134$ й $IMAGE135$ для всіх $IMAGE136$.
буде підгрупою тоді й тільки тоді, коли $IMAGE134$ й $IMAGE135$ для всіх $IMAGE136$.
Нехай $IMAGE137$ - непуста підмножина групи  . Сукупність всіх елементів групи
. Сукупність всіх елементів групи  , з кожним елементом множини $IMAGE137$, називається централізатором множини $IMAGE137$ в групі
, з кожним елементом множини $IMAGE137$, називається централізатором множини $IMAGE137$ в групі  й позначається через $IMAGE143$.
й позначається через $IMAGE143$.
Лема 2 1. Якщо $IMAGE137$ - підмножина групи  , то централізатор $IMAGE143$ є підгрупою.
, то централізатор $IMAGE143$ є підгрупою.
2. Якщо $IMAGE99$ й $IMAGE137$ - підмножина групи  й $IMAGE150$, то $IMAGE151$.
й $IMAGE150$, то $IMAGE151$.
3. Якщо $IMAGE137$ - підмножина групи  й $IMAGE95$, то $IMAGE155$.
й $IMAGE95$, то $IMAGE155$.
Центром групи  називається сукупність всіх елементів з
називається сукупність всіх елементів з  , з кожним елементом групи. Центр позначається через $IMAGE89$. Ясно, що $IMAGE159$, тобто центр групи
, з кожним елементом групи. Центр позначається через $IMAGE89$. Ясно, що $IMAGE159$, тобто центр групи  збігається із централізатором підмножини
збігається із централізатором підмножини  в групі
в групі  . Крім того, $IMAGE163$.
. Крім того, $IMAGE163$.
Зафіксуємо в групі  елемент $IMAGE165$. Перетинання всіх підгруп групи
елемент $IMAGE165$. Перетинання всіх підгруп групи  , що містять елемент $IMAGE165$, назвемо циклічною підгрупою, породженої елементом $IMAGE165$, і позначимо через $IMAGE169$.
, що містять елемент $IMAGE165$, назвемо циклічною підгрупою, породженої елементом $IMAGE165$, і позначимо через $IMAGE169$.
Теорема 3 Циклічна підгрупа $IMAGE170$, породжена елементом $IMAGE165$, складається із усіляких цілих ступенів елемента $IMAGE165$, тобто $IMAGE173$.
Наслідок 4 Циклічна підгрупа абелева.
Нехай $IMAGE165$ - елемент групи  . Якщо всі ступені елемента $IMAGE165$ різні, тобто $IMAGE177$ для всіх цілих $IMAGE178$, то говорять, що елемента $IMAGE165$ має нескінченний порядок.
. Якщо всі ступені елемента $IMAGE165$ різні, тобто $IMAGE177$ для всіх цілих $IMAGE178$, то говорять, що елемента $IMAGE165$ має нескінченний порядок.
Якщо $IMAGE137$ - непуста підмножина групи  й $IMAGE182$ те $IMAGE183$ й $IMAGE184$. Елемент $IMAGE185$ називається перестановочним з підмножиною $IMAGE137$, якщо $IMAGE187$. Рівність $IMAGE187$ означає, що для будь-якого елемента $IMAGE189$ існує такий елемент $IMAGE190$, що $IMAGE191$. Якщо елемент $IMAGE192$ перестановочний з підмножиною $IMAGE137$, то $IMAGE187$ й $IMAGE195$. Сукупність всіх елементів групи
й $IMAGE182$ те $IMAGE183$ й $IMAGE184$. Елемент $IMAGE185$ називається перестановочним з підмножиною $IMAGE137$, якщо $IMAGE187$. Рівність $IMAGE187$ означає, що для будь-якого елемента $IMAGE189$ існує такий елемент $IMAGE190$, що $IMAGE191$. Якщо елемент $IMAGE192$ перестановочний з підмножиною $IMAGE137$, то $IMAGE187$ й $IMAGE195$. Сукупність всіх елементів групи  , перестановочних з підмножиною $IMAGE137$, називається нормалізатором підмножини $IMAGE137$ в групі
, перестановочних з підмножиною $IMAGE137$, називається нормалізатором підмножини $IMAGE137$ в групі  й позначається через $IMAGE200$. Отже,
й позначається через $IMAGE200$. Отже,
$IMAGE201$
5. Нехай $IMAGE137$ - непуста підмножина групи  , $IMAGE192$ - довільний елемент групи
, $IMAGE192$ - довільний елемент групи  . Тоді:
. Тоді:
1) $IMAGE206$;
2) $IMAGE207$;
3) $IMAGE208$;
4) $IMAGE209$;
5) якщо $IMAGE65$ - підгрупа групи  , те $IMAGE212$.
, те $IMAGE212$.
Підгрупа $IMAGE65$ називається нормальною підгрупою групи  , якщо $IMAGE215$ для всіх $IMAGE95$. Запис $IMAGE73$ читається: " $IMAGE65$ - нормальна підгрупа групи
, якщо $IMAGE215$ для всіх $IMAGE95$. Запис $IMAGE73$ читається: " $IMAGE65$ - нормальна підгрупа групи  ". Рівність $IMAGE215$ означає, що для будь-якого елемента $IMAGE221$ існує елемент $IMAGE222$ такий, що $IMAGE223$.
". Рівність $IMAGE215$ означає, що для будь-якого елемента $IMAGE221$ існує елемент $IMAGE222$ такий, що $IMAGE223$.
Теорема. 6 Для підгрупи $IMAGE65$ групи  наступні твердження еквівалентні:
наступні твердження еквівалентні:
1) $IMAGE65$ - нормальна підгрупа;
2) підгрупа $IMAGE65$ разом з кожним своїм елементом містить всі йому сполучені елементи, тобто $IMAGE228$ для всіх $IMAGE95$;
3) підгрупа $IMAGE65$ збігається з кожною своєю сполученою підгрупою, тобто $IMAGE231$ для всіх $IMAGE95$.
Нехай $IMAGE65$ - підгрупа групи  . Тоді:
. Тоді:
1) $IMAGE235$;
2) якщо $IMAGE236$ й $IMAGE237$, те $IMAGE238$;
3) $IMAGE86$ - найбільша підгрупа групи  , у якій $IMAGE65$ нормальна;
, у якій $IMAGE65$ нормальна;
4) якщо $IMAGE73$, те $IMAGE243$. Обернено, якщо $IMAGE243$, те $IMAGE73$;
5) $IMAGE246$ для будь-якої непустої підмножини $IMAGE137$ групи  .
.
У кожній групі  тривіальні підгрупи (одинична підгрупа $IMAGE250$ й сама група
тривіальні підгрупи (одинична підгрупа $IMAGE250$ й сама група  ) є нормальними підгрупами. Якщо в неодиничній групі
) є нормальними підгрупами. Якщо в неодиничній групі  немає інших нормальних підгруп, то група
немає інших нормальних підгруп, то група  називається простій. Одиничну групу $IMAGE250$ вважають непростий.
називається простій. Одиничну групу $IMAGE250$ вважають непростий.
4. Ізометрії
Знакозмінні простори
Векторний простір $IMAGE255$ над полем $IMAGE256$ називається знакозмінним, якщо на ньому задана знакозмінна білінійна форма $IMAGE257$, тобто відображення $IMAGE258$ з наступними властивостями:
$IMAGE259$
$IMAGE260$
$IMAGE261$
$IMAGE262$
для всіх $IMAGE28$, $IMAGE264$, $IMAGE265$ з $IMAGE255$ і всіх $IMAGE267$ з $IMAGE256$. Відзначимо наслідок цих співвідношень: $IMAGE269$. Якщо $IMAGE258$ - знакозмінна форма й $IMAGE267$ - довільний елемент із $IMAGE256$, то відображення $IMAGE273$, певне формулою $IMAGE274$, і складний об'єкт, що є вихідним векторним простором $IMAGE255$ із цією новою формою $IMAGE276$, буде знакозмінним простором, що ми позначимо через $IMAGE277$.
Уявлення знакозмінного простору $IMAGE255$ в знакозмінний простір $IMAGE279$ (обоє над полем $IMAGE256$ і з формами, позначуваними через $IMAGE257$) є по визначенню лінійне перетворення $IMAGE282$ простору $IMAGE255$ в $IMAGE279$, таке, що $IMAGE285$ для всіх $IMAGE28$, $IMAGE287$. Інвективне уявлення називається ізометрією $IMAGE255$ в. $IMAGE279$ Простору $IMAGE255$ й $IMAGE279$ називаються ізометричними, якщо існує ізометрія $IMAGE255$ на $IMAGE279$. Нехай $IMAGE294$ позначає уявлення, $IMAGE295$ - ізометрію ``в'', а $IMAGE296$ або $IMAGE297$ - ізометрію ``на''. Очевидно, що композиція дві ізометрії - ізометрія й перетворення, зворотне до ізометрії, - також ізометрія. Зокрема, множину ізометрій простору $IMAGE255$ на себе є підгрупою загальної лінійної групи $IMAGE299$ абстрактного векторного простору $IMAGE255$; вона називається симплектичною групою знакозмінного простору $IMAGE255$ й позначається через $IMAGE302$. Для будь-якого ненульового елемента $IMAGE267$ з $IMAGE256$ маємо $IMAGE305$.
Пропозиція.7 Нехай $IMAGE282$ - лінійне перетворення знакозмінного простору $IMAGE255$ в знакозмінний простір $IMAGE279$. Припустимо, що існує база $IMAGE309$ простору $IMAGE255$, така, що $IMAGE311$ для всіх $IMAGE312$, $IMAGE313$. Тоді $IMAGE282$ - уявлення.
Доказ. Це тривіально треба з визначень.
Кожному знакозмінному простору $IMAGE255$ зі знакозмінною формою $IMAGE257$ зіставимо відображення $IMAGE317$ й $IMAGE318$ простори $IMAGE255$ в сполучений простір $IMAGE320$ ( $IMAGE255$ розглядається як абстрактний векторний простір над $IMAGE256$). По визначенню відображення $IMAGE317$ зіставляє довільному елементу $IMAGE28$ з $IMAGE255$ лінійний функціонал $IMAGE326$, певний формулою $IMAGE327$, а $IMAGE318$ переводить $IMAGE28$ в. $IMAGE330$ Легко перевіряється, що $IMAGE331$ і $IMAGE332$ є лінійними перетвореннями.
$IMAGE333$ - матриця 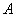 над $IMAGE256$ називається косо симетричною, якщо $IMAGE336$, і знакозмінної, якщо $IMAGE336$ й на головній діагоналі коштують нулі. Таким чином, знакозмінні матриці є косо симетричними. Обернено, косо симетричні матриці є знакозмінними, якщо характеристика поля $IMAGE256$ не дорівнює $IMAGE339$. Розглянемо знакозмінний простір $IMAGE255$. Ми можемо асоціювати з базою $IMAGE309$ простору $IMAGE255$ матрицю, у якої на місці $IMAGE343$ коштує $IMAGE344$. Назвемо
над $IMAGE256$ називається косо симетричною, якщо $IMAGE336$, і знакозмінної, якщо $IMAGE336$ й на головній діагоналі коштують нулі. Таким чином, знакозмінні матриці є косо симетричними. Обернено, косо симетричні матриці є знакозмінними, якщо характеристика поля $IMAGE256$ не дорівнює $IMAGE339$. Розглянемо знакозмінний простір $IMAGE255$. Ми можемо асоціювати з базою $IMAGE309$ простору $IMAGE255$ матрицю, у якої на місці $IMAGE343$ коштує $IMAGE344$. Назвемо 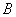 матрицею знакозмінного простору $IMAGE255$ в базі $IMAGE309$ й будемо писати $IMAGE348$
матрицею знакозмінного простору $IMAGE255$ в базі $IMAGE309$ й будемо писати $IMAGE348$
Якщо існує хоча б одна база, у якій $IMAGE255$ має матрицю 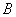 , то будемо писати $IMAGE351$. Матриця
, то будемо писати $IMAGE351$. Матриця 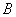 , асоційована зі знакозмінним простором $IMAGE255$ зазначеним способом, є, мабуть, знакозмінної. Що відбувається при зміні бази? Припустимо, що $IMAGE354$ в базі $IMAGE355$ й $IMAGE356$ - матриця переходу від першої бази до другого, тобто $IMAGE357$. Тоді $IMAGE358$ звідки видно, що зміна матриці простору $IMAGE255$ при зміні бази описується співвідношенням $IMAGE360$.
, асоційована зі знакозмінним простором $IMAGE255$ зазначеним способом, є, мабуть, знакозмінної. Що відбувається при зміні бази? Припустимо, що $IMAGE354$ в базі $IMAGE355$ й $IMAGE356$ - матриця переходу від першої бази до другого, тобто $IMAGE357$. Тоді $IMAGE358$ звідки видно, що зміна матриці простору $IMAGE255$ при зміні бази описується співвідношенням $IMAGE360$.
Якщо $IMAGE255$ - абстрактний векторний простір з базою $IMAGE309$ й 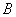 - довільна знакозмінна $
- довільна знакозмінна $